Diagrama de temas
-
-
Foro
-
-

 Esta rama de la mecánica de fluidos se
ocupa de las leyes de los fluidos en movimiento. Euler fue el
primero en reconocer que las leyes dinámicas para los fluidos
sólo pueden expresarse de forma relativamente sencilla si se
supone que el fluido es incompresible e ideal, es decir, si se
pueden despreciar los efectos del rozamiento y la viscosidad. Sin
embargo, como esto nunca es así en el caso de los fluidos reales
en movimiento, los resultados de dicho análisis sólo pueden
servir como estimación para flujos en los que los efectos
de la viscosidad son pequeños.
Esta rama de la mecánica de fluidos se
ocupa de las leyes de los fluidos en movimiento. Euler fue el
primero en reconocer que las leyes dinámicas para los fluidos
sólo pueden expresarse de forma relativamente sencilla si se
supone que el fluido es incompresible e ideal, es decir, si se
pueden despreciar los efectos del rozamiento y la viscosidad. Sin
embargo, como esto nunca es así en el caso de los fluidos reales
en movimiento, los resultados de dicho análisis sólo pueden
servir como estimación para flujos en los que los efectos
de la viscosidad son pequeños.
TIPOS DE FLUIDOS
- Flujo de fluidos a régimen permanente o intermitente: aquí se tiene en cuenta la velocidad de las partículas del fluido, ya sea esta constante o no con respecto al tiempo
- Flujo de fluidos compresible o incompresible: se tiene en cuenta a la densidad, de forma que los gases son fácilmente compresibles, al contrario que los líquidos cuya densidad es prácticamente constante en el tiempo.
- Flujo de fluidos viscoso o no viscoso: el viscoso es aquel que no fluye con facilidad teniendo una gran viscosidad. En este caso se disipa energía.
Llamamos fluido ideal a aquel que fluye sin dificultad alguna, aquel cuya viscosidad vale cero. Tal fluido no existe pero en ciertas circunstancias -en las que resulta una razonable aproximación a la realidad- se pueden aplicar algunas de sus propiedades y leyes de movimiento a los fluidos de verdad.
Definamos con más precisión algunas de sus propiedades:
- Viscosidad cero
- Son incompresibles (su densidad es constante)
- El flujo es laminar (más adelante ahondaremos este concepto, pero lo que aquí importa es que se desplaza ordenadamente sin hacer remolinos, ni reflujos)
- La velocidad de todas las moléculas del fluido en una sección transversal de tubería es la misma.
Algunas consideraciones:
- Cuando un flujo no cambia con el correr del tiempo se llama estacionario.
- El fluido de un líquido ideal estacionario es aquel en el que se conserva la energía mecánica (esta es una definición sumamente operativa).
CAUDAL VOLUMÉTRICO, Q
 La medida fundamental que
describe el movimiento de un fluido es el caudal.
La medida fundamental que
describe el movimiento de un fluido es el caudal.
 Decir que el río es más
caudaloso que otro indica que el primero transporta más agua que
el segundo en la misma cantidad de tiempo.
Decir que el río es más
caudaloso que otro indica que el primero transporta más agua que
el segundo en la misma cantidad de tiempo.
A su vez, la cantidad de fluido puede medirse por su masa o por su volumen (siempre que su densidad sea constante, cosa que supondremos que es así), de modo que:
caudal
=
volumen
Q
=
Vol
(caudal de volumen)
tiempo
Δt
Al usar la segunda expresión, que se medirá en unidades de volumen sobre unidades de tiempo. Las unidades en el Sistema Internacional es:
Q= Vol / Δt = [m3/s]
El caudal se relaciona fácilmente con la velocidad a la que se desplaza el fluido. Consideremos un tubo por el que se desplaza un fluido. La sección interna (o área) del tubo es A y la velocidad a la que se desplaza el fluido (cada molécula del fluido) es v. Ahora tomemos arbitrariamente un cierto volumen dentro del tubo. Ese volumen (un cilindro) es igual a la superficie de su base (que no es otro que la sección del tubo, A) por la altura (un cierto d):
Vol = A . d

Al cabo de cierto intervalo de tiempo (Δt) todo el volumen habrá atravesado el área de adelante. Justamente así teníamos definido el caudal: Q = Vol / Δt
y recordando que v = d/Δt nos queda:
Q = A . v
El caudal es igual a la velocidad a la que se mueve el fluido por la sección del conducto.
Donde:
- Q, Caudal [m3/s]
- A, Es el área [m2]
- v, Es la velocidad lineal promedio [m/s]
PRINCIPIO DE CONTINUIDAD
 Supongamos que a una llave
abierta que posee un cierto caudal le enchufamos una manguera.
Después de un rato en que nos aseguramos que el flujo se
estabiliza (o sea: logramos un flujo estacionario) no está mal
decir que la llave vierte en un extremo de la manguera
una cierta cantidad de agua en una cierta cantidad de tiempo.
Ejemplo, 10 litros por minuto. ¿Cuál es el caudal en el otro
extremo de la manguera? 10 litros por minuto. La misma cantidad
que entra por una punta sale por el otro extremo en el mismo
intervalo de tiempo.
Supongamos que a una llave
abierta que posee un cierto caudal le enchufamos una manguera.
Después de un rato en que nos aseguramos que el flujo se
estabiliza (o sea: logramos un flujo estacionario) no está mal
decir que la llave vierte en un extremo de la manguera
una cierta cantidad de agua en una cierta cantidad de tiempo.
Ejemplo, 10 litros por minuto. ¿Cuál es el caudal en el otro
extremo de la manguera? 10 litros por minuto. La misma cantidad
que entra por una punta sale por el otro extremo en el mismo
intervalo de tiempo.
Señalar esto es lo mismo que decir: en todo el trayecto de la manguera no se crea ni se destruye agua. Todo lo que entra, sale. A esta cuestión tan sencilla se la llama principio o ecuación de continuidad y no es nada más ni nada menos que la forma que adopta el principio de conservación de la materia en los fluidos.
Si llamamos Q1 al caudal en un extremo y Q2 al caudal en el otro podemos resumir todo lo dicho escribiendo:
Q1 = Q2

Si combinamos esta obviedad -fundamental- con la relación velocidad-área nos queda:
A1 . v1 = A2 . v2
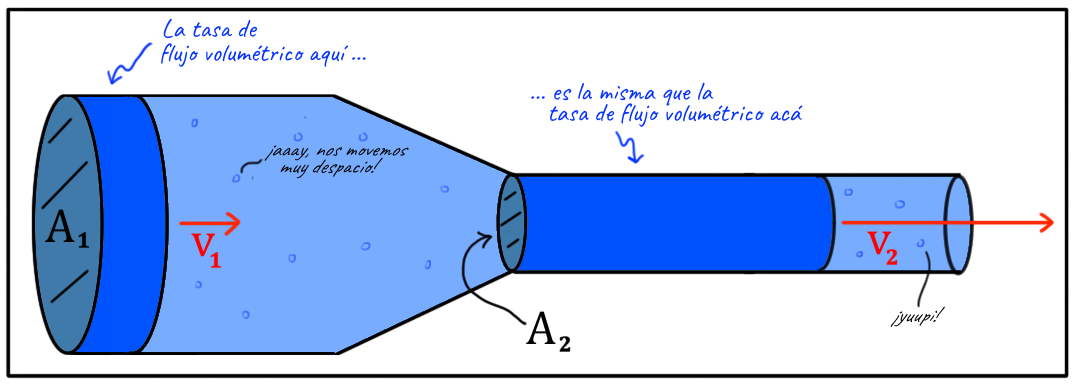
Esta expresión nos dice que en todas las partes de la manguera el líquido se va a mover a la misma velocidad, mientras no cambie la sección de la manguera. Pero por otro lado, también nos dice que en todo conducto de sección variable...
Cuando aumenta la sección disminuye la velocidad,cuando disminuye
la sección aumenta la velocidad.
FLUJO LAMINAR Y TURBULENTO
 Otro concepto de
importancia en el tema son las líneas de corriente que sirven
para representar la trayectoria de las partículas del fluido.
Esta se define como una línea trazada en el fluido, de modo que
una tangente a la línea de corriente en cualquier punto sea
paralela a la velocidad del fluido en tal punto. Dentro de las
líneas de corriente se puede determinar una región tubular del
fluido cuyas paredes son líneas de corriente. A esta región se le
denomina tubo de flujo.
Otro concepto de
importancia en el tema son las líneas de corriente que sirven
para representar la trayectoria de las partículas del fluido.
Esta se define como una línea trazada en el fluido, de modo que
una tangente a la línea de corriente en cualquier punto sea
paralela a la velocidad del fluido en tal punto. Dentro de las
líneas de corriente se puede determinar una región tubular del
fluido cuyas paredes son líneas de corriente. A esta región se le
denomina tubo de flujo.
TIPOS DE FLUJOS EN FLUIDOS



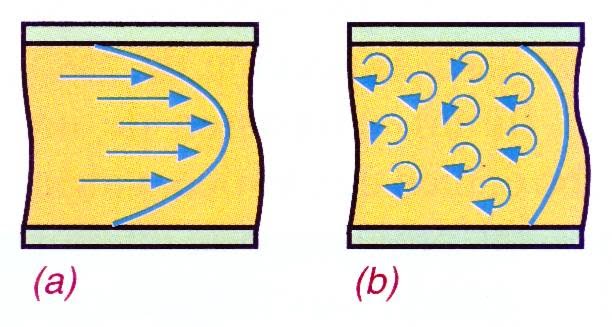


Flujo laminar: Ocurre cuando las moléculas de un fluido en movimiento siguen trayectorias paralelas, o sea, se deslizan suavemente unas sobre otras, sin que exista mezcla macroscópica o intercambio transversal entre ellas.

Flujo turbulento: Ocurre cuando las moléculas de un fluido en movimiento forman torbellinos, produciendo un flujo inestable.


ECUACIÓN DE BERNOULLI
Daniel Bernoulli (1700-1782), descubrió la fórmula llamamos simplemente Principio de Bernoulli.
Esta ecuación surge de la aplicación del principio de conservación de la energía mecánica, pero aplicada a un fluido. Por caso general tomemos una corriente en un tubo de ancho variable que además cambia de altura.
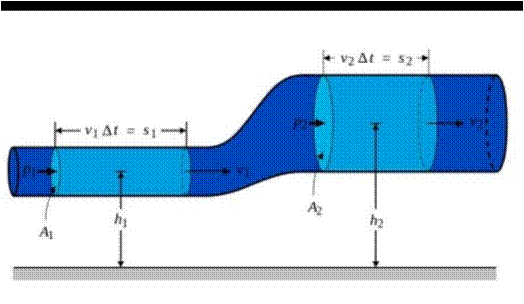
En esta corriente de fluido ideal se cumple que:

Analicemos por separado cada uno de los tres términos:
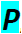 , el primero. P es presión, y representa al trabajo que realiza
sobre una masa de fluido, la masa de fluido de atrás que viene
empujando. Proviene de dividir el trabajo de una fuerza exterior
(W) sobre una masa de fluido, por su volumen.
, el primero. P es presión, y representa al trabajo que realiza
sobre una masa de fluido, la masa de fluido de atrás que viene
empujando. Proviene de dividir el trabajo de una fuerza exterior
(W) sobre una masa de fluido, por su volumen.
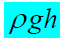 , el segundo. Densidad por gravedad
por altura. Este término representa la energía potencial del
fluido: la energía que posee simplemente por estar a cierta
altura sobre la Tierra. Proviene de dividir la energía potencial
gravitatoria de una masa cualquiera de fluido, m
g h, por su volumen.
, el segundo. Densidad por gravedad
por altura. Este término representa la energía potencial del
fluido: la energía que posee simplemente por estar a cierta
altura sobre la Tierra. Proviene de dividir la energía potencial
gravitatoria de una masa cualquiera de fluido, m
g h, por su volumen.
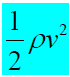 , el tercero. Un medio por la densidad
por la velocidad de la corriente al cuadrado. Este término
representa la energía cinética del fluido. Proviene de dividir la
energía cinética, ½ m v², por el volumen. A este término se le
llama presión
hidrodinámica.
, el tercero. Un medio por la densidad
por la velocidad de la corriente al cuadrado. Este término
representa la energía cinética del fluido. Proviene de dividir la
energía cinética, ½ m v², por el volumen. A este término se le
llama presión
hidrodinámica.
Se puede concluir que el Principio de Bernoulli viene a ser algo así como el aspecto que el principio de conservación de la energía mecánica adopta en los fluidos. Y a eso se llega dividiendo la energía mecánica del fluido por su volumen. Algo así como energía mecánica por unidad de volumen: la energía mecánica específica.
Se debe recordar la energía mecánica se conserva sólo cuando no hay fuerzas no conservativas actuando (WNC = ΔEM), de modo que el principio de Bernoulli sólo puede aplicarse a fluidos en los que la viscosidad (el rozamiento) sea despreciable.
El principio de Bernoulli sólo se puede aplicar a fluidos ideales
Aún así representa una herramienta muy útil, y sumamente descriptiva.
Que la suma de los tres términos sea constante nos permite comparar dos estados, dos posiciones de una misma corriente:

ALGUNAS CONSIDERACIONES:
La figura muestra una tubería en la que pueden variar las secciones y las alturas por las que circula.

Recordar que se trata de un fluido ideal con densidad constante y flujo ordenado.
Veamos dos casos particulares y muy aleccionadores.
- Primero supongamos que el fluido está quieto.

En ese caso vA = vB = 0, los términos de energía cinética desaparecen y nos queda:

reagrupando

- Ahora analicemos que pasa con una corriente horizontal, es decir, sin cambios de altura.

Cuando hA es igual a hB, los segundos términos se cancelan y nos queda
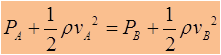
Es decir, cuando la corriente va más rápido la presión es menor. Este resultado algunas veces parece contrario a nuestra intuición; sin embargo explica un montón de fenómenos interesantes como el vuelo de los aviones.
APLICACIONES DE LA ECUACIÓN DE BERNOULLI
VUELO DE AVIONES


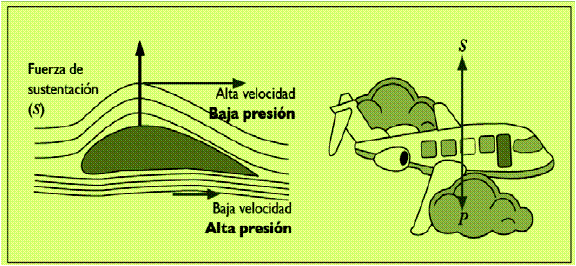
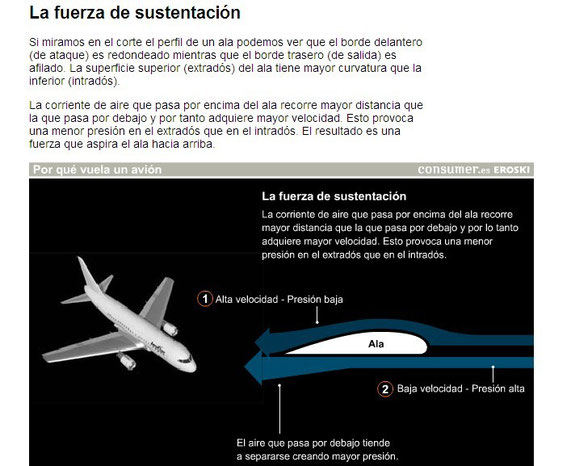
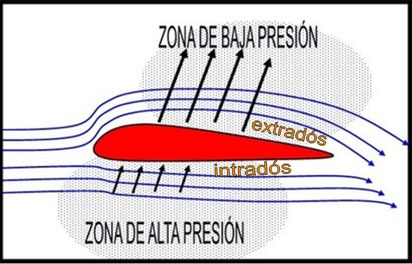
La ecuación de Bernoulli señala que la suma de la presión, la energía cinética por unidad de volumen y la energía potencial gravitatoria por unidad de volumen, es una constante a lo largo de la línea del flujo.


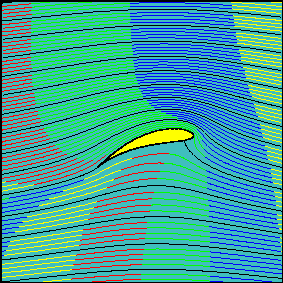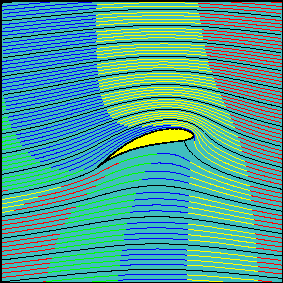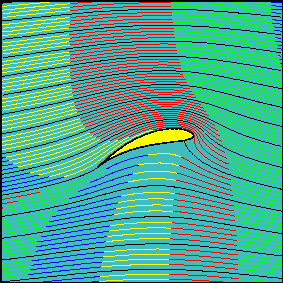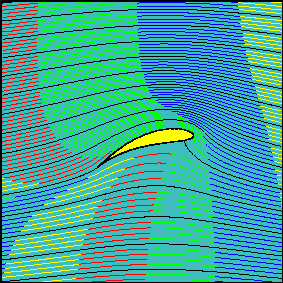

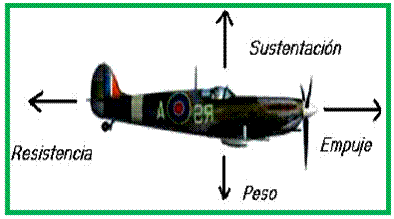
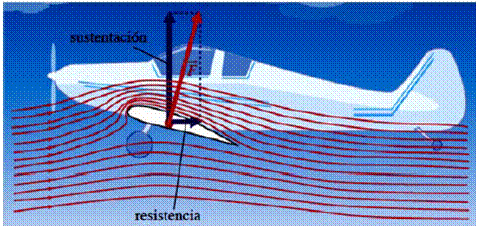
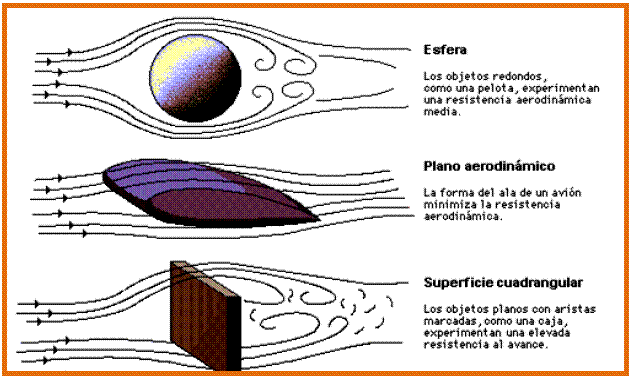
Este principio explica el vuelo de los aviones, ya que la forma y la orientación de las alas permiten que el aire pase con mayor rapidez por la parte superior que la inferior de éstas.
Luego, la presión encima del ala es menor que la presión debajo de ella, produciendo una fuerza resultante dirigida hacia arriba, llamada fuerza ascensional o de sustentación (S).

 En los automóviles de
carrera se busca el efecto contrario de los aviones. Se trata de
obtener una fuerza ascendente que es producida por el paso de
aire debajo de los autos cuando dicho aire no es conducido hacia
la parte trasera y este sale por los laterales del fondo de los
autos. En esto
En los automóviles de
carrera se busca el efecto contrario de los aviones. Se trata de
obtener una fuerza ascendente que es producida por el paso de
aire debajo de los autos cuando dicho aire no es conducido hacia
la parte trasera y este sale por los laterales del fondo de los
autos. En esto

se centra una de las principales funciones de los Ingenieros de los equipos de competencia y es tratar de conducir el aire debajo de los coches hacia un difusor trasero para aumentar la velocidad del aire y de esta manera crear succión y que el aire no salga por los laterales creando down force para contrarrestar la fuerza ascendente.
Esto es lo que sucede en un auto cuando la fuerza ascendente es mayor que la descendente.

EFECTO MAGNUS
Consideremos un cilindro (o una esfera) en un fluido en movimiento. Si el cilindro rota en torno a un eje perpendicular a la corriente del fluido, y además hay roce viscoso entre el cilindro y el fluido, entonces el cilindro arrastrará al fluido haciendo que las velocidades del fluido a ambos lados del cilindro no sean iguales.
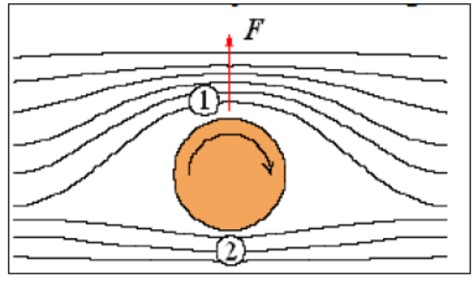
En el caso mostrado en la figura adjunta, la velocidad es mayor arriba que abajo. De acuerdo a la ecuación de Bernoulli, la presión en el lugar 1 serán inferior que en el lado 2 (p1 < p2).
Esta diferencia de presión genera una fuerza neta sobre el cilindro hacia arriba. Es este efecto, llamado efecto Magnus, el responsable de los así llamados “efectos” que pueden observarse en numerosos
juegos de pelota.
Suponga que una bola es pateada de tal manera que va rotando a la derecha sobre un perpendicular del eje a su dirección móvil durante su movimiento a la izquierda (véase la figura). Entonces la bola experimentaría la fuerza de Magnus. Así la bola se mueve con una trayectoria curvada hacia la derecha
del arquero.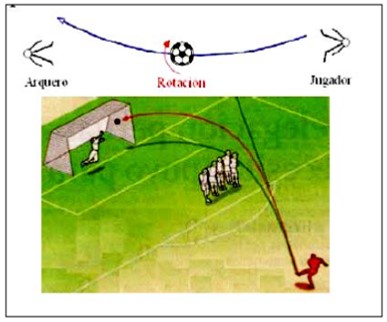



PELOTA DE GOLF CON HOYUELOS


Lo primero que tenemos que tener presente es que cuando un objeto se mueve a través del aire, obliga a que este se “separe”.
 En este principio radica el
sentido por el cual la bola de golf tiene hoyuelos, ya que una
esfera (bola) lisa produce un “flujo laminar” (que no es agitado
sino más bien suave y ordenado) conforme se mueve a través del
aire. Esto produce un tipo de resistencia del aire (causada por
la presión) que hace que la bola pierda velocidad.
En este principio radica el
sentido por el cual la bola de golf tiene hoyuelos, ya que una
esfera (bola) lisa produce un “flujo laminar” (que no es agitado
sino más bien suave y ordenado) conforme se mueve a través del
aire. Esto produce un tipo de resistencia del aire (causada por
la presión) que hace que la bola pierda velocidad.
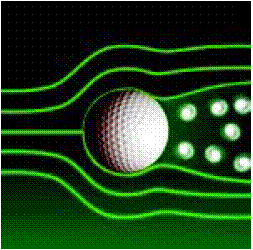 Por el contrario, una
superficie áspera o con hoyuelos produce un flujo turbulento
(agitado y desordenado). La separación del flujo turbulento es
menor que la del flujo laminar. La resistencia del aire causada
por la presión es, por lo tanto, menor. Así la bola de golf (que
tiene hoyuelos) vuela más lejos que si no los tuviese. Una bola
menor vuela a mayor distancia al ofrecer menos resistencia y del
mismo modo tomará mayores efectos.
Por el contrario, una
superficie áspera o con hoyuelos produce un flujo turbulento
(agitado y desordenado). La separación del flujo turbulento es
menor que la del flujo laminar. La resistencia del aire causada
por la presión es, por lo tanto, menor. Así la bola de golf (que
tiene hoyuelos) vuela más lejos que si no los tuviese. Una bola
menor vuela a mayor distancia al ofrecer menos resistencia y del
mismo modo tomará mayores efectos.
- Una bola en un chorro de aire
Una bola ligera se puede mantenido en un chorro de aire como se muestra en la figura. Una pelota de ping-pong puede hacerse flotar sobre un chorro de aire (algunas aspiradoras pueden soplar aire), si la pelota comienza a dejar el chorro de aire, la presión más alta de afuera del chorro empuja la pelota de nuevo hacia éste como se muestra en la figura siguiente.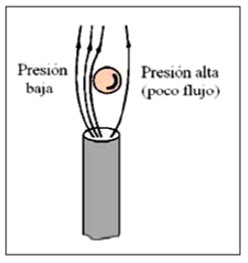

- LEVANTAR UNA BOLA CON UN EMBUDO.
En el espacio entre la superficie del embudo y la superficie de la bola la presión es menor que la presión atmosférica, y esta diferencia de presión soporta la bola contra la acción de la gravedad.
Una bola ligera apoyada por un jet del aire. La presión sobre la bola es menos que debajo de ella.

- EL ATOMIZADOR

Algunos dispositivos operan mediante los diferenciales de presión que resultan de las diferencias en la rapidez de un fluido. Por ejemplo, una corriente de aire que pasa sobre un extremo abierto de un tubo, con el otro extremo sumergido en un líquido, reduce la presión sobre el tubo, como se ilustra en la figura.
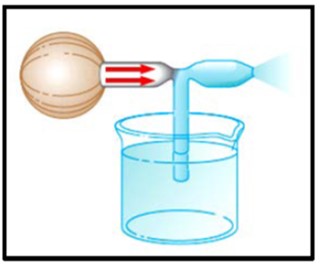
Esta reducción en presión hace que el líquido se eleve en la corriente del aire. Por lo tanto el líquido se dispersa en un fino rocío de gotitas. Usted puede identificar que este atomizador se usa en botellas de perfume y rociadores de pintura.
La presión en el aire soplado a alta velocidad a través de la parte superior del tubo vertical de atomizador. Un atomizador de perfume o de un rociador de insecticida es menor que la presión normal del aire que actúa sobre la superficie del líquido en el frasco, así el perfume es empujado hacia arriba del tubo debido a la presión reducida en la parte superior.
- Efecto chimenea
 ¿Por qué sube el humo por
una chimenea? En parte se debe a que el aire caliente se
eleva (es decir, debido a la
densidad). Pero el principio de Bernoulli también tiene un
lugar importante. Debido a que el
viento sopla a través de la parte superior de la chimenea,
la presión es menor ahí que dentro
de la casa. Por eso el aire y el humo son empujados
hacia arriba de la chimenea. Incluso
en una noche calmada, existe el flujo de aire suficiente en
el ambiente en el extremo superior
de una chimenea para permitir el flujo ascendente
del humo.
¿Por qué sube el humo por
una chimenea? En parte se debe a que el aire caliente se
eleva (es decir, debido a la
densidad). Pero el principio de Bernoulli también tiene un
lugar importante. Debido a que el
viento sopla a través de la parte superior de la chimenea,
la presión es menor ahí que dentro
de la casa. Por eso el aire y el humo son empujados
hacia arriba de la chimenea. Incluso
en una noche calmada, existe el flujo de aire suficiente en
el ambiente en el extremo superior
de una chimenea para permitir el flujo ascendente
del humo.
Si las tuzas, perros de la pradera, conejos y otros animales que viven bajo el no se asfixian, el aire debe circular en sus madrigueras. Estas siempre tienen por lo menos dos entradas.
La velocidad del flujo del aire a través de los diferentes hoyos por lo regular será un poco distinta. Esto conduce a una pequeña diferencia de presión que fuerza al flujo de aire a través de la madriguera por el principio de Bernoulli. El flujo de aire se intensifica si un hoyo está más arriba que el otro (lo que a menudo hacen los animales) puesto que la velocidad del viento tiende a incrementarse con la altura.
- La ventilación en una mina
La ventilación en una mina responde a tres propósitos principales: para proporcionar el aire fresco para la respiración de los mineros, diluir los gases nocivos que puedan ser formados subterráneamente.
En un túnel horizontal simple de minería generalmente es suficiente la ventilación natural utilizando la diferencia en la presión de aire asociada a la diferencia en nivel entre dos aberturas, la entrada de la mina y la parte superior de un eje de ventilación (efecto chimenea).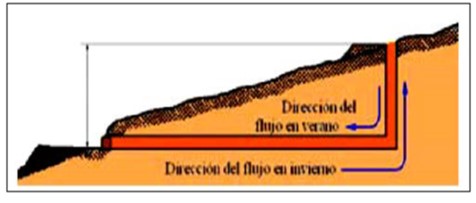
- Sistema cardiovascular
 La física de los fluidos
tiene muchas aplicaciones en los sistemas biológicos, como por ejemplo en la
estimación de la presión sanguínea,
donde se puede utilizar la ecuación
de Bernoulli.
La física de los fluidos
tiene muchas aplicaciones en los sistemas biológicos, como por ejemplo en la
estimación de la presión sanguínea,
donde se puede utilizar la ecuación
de Bernoulli.
El instrumento para medir la presión sanguínea se llama esfigmomanómetro, que utiliza el principio de Pascal.
- Arteria o vena con una obstrucción
Parece que en la medicina es bastante común que las arterias o las venas se taponen con cosas tipo colesterol y demás.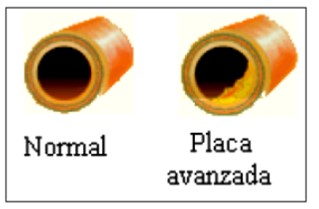
Concretamente la situación es esta:
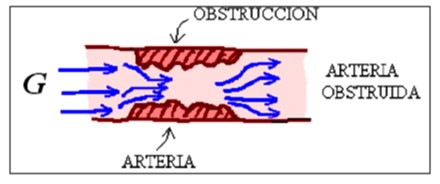

Si se le pregunta a una persona que cree que va a ocurrir con la arteria cuando se obstruye, la respuesta más común es esta: La sangre se va a frenar al chocar con la obstrucción, y va a empezar a presionar hacia fuera porque quiere pasar. Por lo tanto la arteria se va a dilatar y se va a formar como un globo. Este razonamiento es muy lindo y muy intuitivo pero está MAL. Lo que pasa es justo al revés. El caudal que manda el corazón es constante. Este caudal no se frena por ningún motivo.
Para poder pasar por la obstrucción lo que hace la sangre es aumentar su velocidad. (La velocidad aumenta porque el diámetro de la arteria disminuye).
Al aumentar la velocidad dentro de la arteria, la presión adentro tiene que disminuir. Pero afuera de la arteria la presión sigue siendo la misma. Entonces la presión de afuera le gana a la presión de adentro y la arteria se comprime.
¿Y qué pasa al comprimirse la arteria?
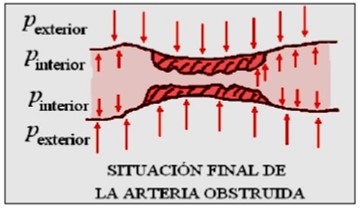 La obstrucción se cierra
más. Esto provoca un aumento de la
velocidad dentro de la obstrucción,
lo que a su vez obliga a la arteria a cerrarse más todavía.
La obstrucción se cierra
más. Esto provoca un aumento de la
velocidad dentro de la obstrucción,
lo que a su vez obliga a la arteria a cerrarse más todavía.
De esta manera, la arteria se va cerrando más y más hasta que sobreviene el colapso.
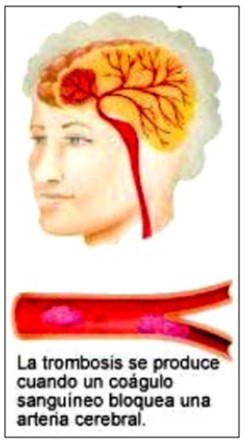
Esto significa que la arteria tiende a cerrarse del todo e impide el pasaje de sangre.
Esto es lo que ocurre cuando una persona tiene un ataque cardíaco. También pasa en el cerebro y en otros lados. Los médicos lo llaman trombosis.
Dependiendo del tamaño y localización del trombo pueden variar algunos de los síntomas, dolor, isquemia, frialdad, ausencia de pulso, etc.
TEOREMA DE TORRICELLI
En la figura un líquido sale de un orificio situado cerca del fondo de un tanque abierto. Su rapidez cuando sale del orificio puede determinarse a partir de la ecuación de Bernoulli. Debemos suponer que el nivel del líquido en el tanque desciende lentamente en comparación con la velocidad de salida, de tal modo que la velocidad v2 en la parte superior puede considerarse cero. Además, debe tomarse en cuenta que la presión del líquido tanto en la parte superior, como en el orificio, es igual a la presión atmosférica. Entonces,
P1 = P2 y v2 = 0, lo que reduce la ecuación de Bernoulli a
O bien
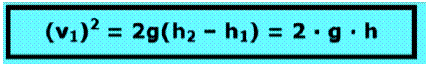
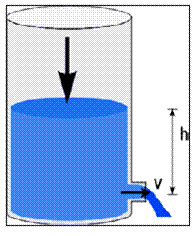
Esta relación se conoce como teorema de Torricelli:

Note que la rapidez de salida de un líquido a la profundidad h es la misma que la que de un objeto que se dejara caer del reposo desde una altura h. La relación de Torricelli nos permite expresar el caudal en términos de la altura del líquido sobre el orificio. O sea:

Un ejemplo interesante para comprobar el principio de Torricelli se muestra en la figura.

La velocidad de descarga aumenta con la profundidad. El alcance máximo se logra cuando la abertura se encuentra en la mitad de la columna de agua. Aunque la velocidad de descarga aumenta por debajo del punto medio, el agua golpea el piso más cerca. Esto ocurre porque llega al piso más pronto. Las perforaciones equidistantes por encima y por abajo del punto medio tendrán el mismo alcance horizontal.
En conclusión la velocidad de descarga aumenta con la profundidad por debajo de la superficie, pero el alcance es máximo en el punto medio.
“La velocidad con la que sale un líquido por un orificio es mayor conforme aumenta la profundidad”.
Cuando se hace un orificio en uno de los lados de un recipiente se destruye la presión de la pared en ese punto y la presión del líquido interior empuja directamente hacia el orificio dándole una aceleración hacia fuera y normal al plano del mismo.
Tubo de Venturi: En la figura se muestra este tipo de tubos, donde se observa que y1 = y2 por lo tanto la ecuación de Bernoulli se reduce a

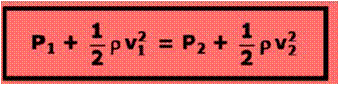
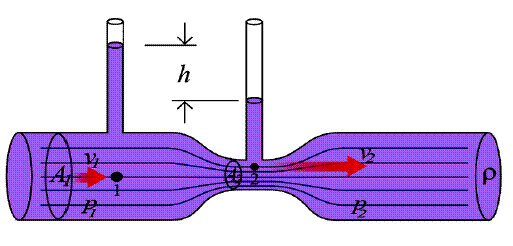

Así en su forma más simple el principio de Bernoulli dice que cuando la rapidez del fluido aumenta su presión disminuye y viceversa.
En el tubo de Venturi en su parte más estrecha sabemos que su velocidad es mayor, por lo que nos dice la ecuación de continuidad, luego usando Bernoulli su presión es menor.
Es común utilizar este tipo de tubos para medir la velocidad de flujo en un fluido incompresible.

-
-
-