Diagrama de temas
-
-
Foro
-
-
-
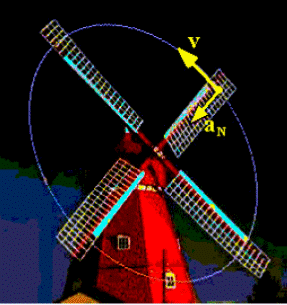
Se define como movimiento circular aquél cuya trayectoria es una circunferencia.
El movimiento circular, llamado también curvilíneo, es otro tipo de movimiento sencillo.
 Estamos rodeados por
objetos que describen movimientos circulares: un disco compacto
durante su reproducción en el equipo de música, las manecillas
de un reloj o las ruedas de una motocicleta son ejemplos de
movimientos circulares; es decir, de cuerpos que se mueven
describiendo una circunferencia.
Estamos rodeados por
objetos que describen movimientos circulares: un disco compacto
durante su reproducción en el equipo de música, las manecillas
de un reloj o las ruedas de una motocicleta son ejemplos de
movimientos circulares; es decir, de cuerpos que se mueven
describiendo una circunferencia.
 A veces el
movimiento circular no es completo: cuando un coche o cualquier
otro vehículo toma una curva realiza un movimiento circular,
aunque nunca gira los 360º de la circunferencia.
A veces el
movimiento circular no es completo: cuando un coche o cualquier
otro vehículo toma una curva realiza un movimiento circular,
aunque nunca gira los 360º de la circunferencia.
La experiencia nos dice que todo aquello da vueltas tiene movimiento circular. Si lo que gira da siempre el mismo número de vueltas por segundo, decimos que posee movimiento circular uniforme (MCU).
Ejemplos de cosas que se mueven con movimiento circular uniforme hay muchos:


La tierra es uno de ellos. Siempre da una vuelta sobre su eje cada 24 horas. También gira alrededor del sol y da una vuelta cada 365 días. Un ventilador, un lavarropas o los viejos tocadiscos, la rueda de un auto que viaja con velocidad constante, son otros tantos ejemplos.
Pero no debemos olvidar que también hay objetos que giran con movimiento circular variado, ya sea acelerado o decelerado.EL MOVIMIENTO CIRCULAR EN MAGNITUDES ANGULARES
 La descripción de un
movimiento circular puede hacerse bien en función de magnitudes
lineales ignorando la forma de la trayectoria (y tendremos
velocidad y aceleración tangenciales), o bien en función de
magnitudes angulares (y tendremos velocidad y aceleración
angulares). Ambas descripciones están relacionadas entre sí
mediante el valor del radio de la circunferencia
trayectoria.
La descripción de un
movimiento circular puede hacerse bien en función de magnitudes
lineales ignorando la forma de la trayectoria (y tendremos
velocidad y aceleración tangenciales), o bien en función de
magnitudes angulares (y tendremos velocidad y aceleración
angulares). Ambas descripciones están relacionadas entre sí
mediante el valor del radio de la circunferencia
trayectoria.
Al trabajar con magnitudes angulares es imprescindible entender lo relativo a una unidad de medida angular conocida como radián.
El radián
 Si tenemos un
ángulo cualquiera y queremos saber cuánto mide, tomamos un
transportador y lo medimos. Esto nos da el ángulo medido en
grados. Este método viene de dividir la circunferencia en 360º,
y se denomina sexagesimal.
Si tenemos un
ángulo cualquiera y queremos saber cuánto mide, tomamos un
transportador y lo medimos. Esto nos da el ángulo medido en
grados. Este método viene de dividir la circunferencia en 360º,
y se denomina sexagesimal.
El sistema de grados sexagesimales es una manera de medir ángulos, pero hay otros métodos, y uno de ellos es usando radianes.
 Es decir:
Es decir:
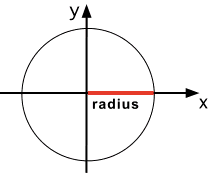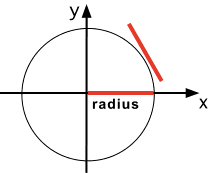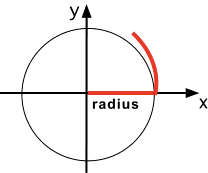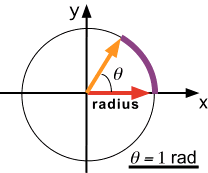
Un radián es el ángulo formado por un arco igual a su radio.
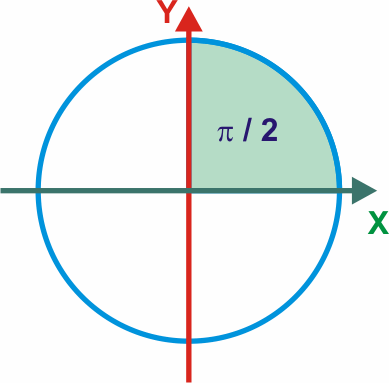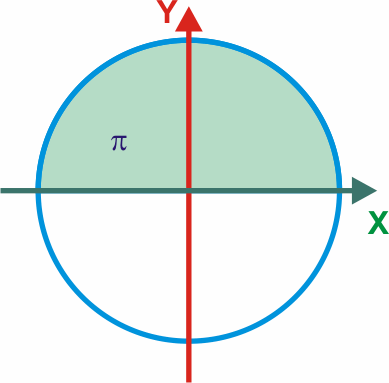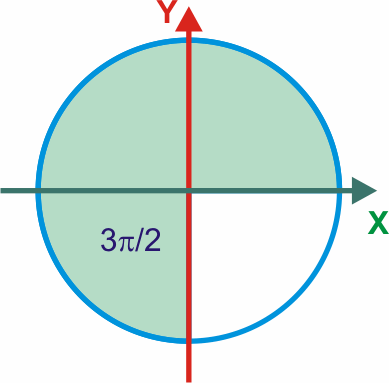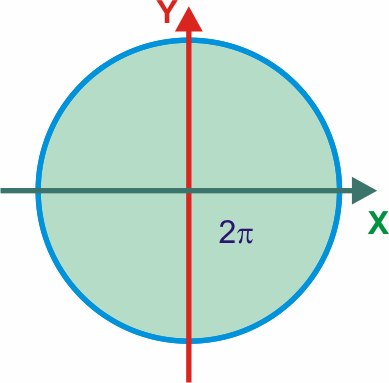
2π radianes = 360°
π radianes = 180°
π/2 radianes = 90°
1 radián = 360° / 2π = 57,3°PERIODO Y FRECUENCIA
La principal característica del movimiento circular uniforme es que en cada vuelta o giro completo de 360°, equivalente a un ciclo, se puede establecer un punto fijo como inicio y fin del ciclo. En física, los ciclos son también llamados revoluciones para un determinado tiempo.
El periodo (T) de un movimiento circular es el tiempo que tarda una partícula o un cuerpo en realizar una vuelta completa, revolución o ciclo completo.
T= Tiempo/ oscilación
Por ejemplo, el periodo de rotación de la tierra es 24 horas. El periodo de rotación de la aguja grande del reloj es de 1 hora. La unidad utilizada para el periodo es el segundo o, para casos mayores, unidades mayores.
Conocida la frecuencia (en ciclos o revoluciones por segundo) se puede calcular el periodo (T) mediante la fórmula: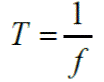
Se denomina frecuencia (f) de un movimiento circular al número de revoluciones, vueltas o ciclos completos durante la unidad de tiempo. La unidad utilizada para cuantificar (medir) la frecuencia de un movimiento es el hertz (Hz), que indica el número de revoluciones o ciclos por cada segundo.
Para su cálculo, usamos la fórmula:
(En ocasiones se usa, en vez de hertz, s−1). Nótese que la frecuencia (f) es la inversa del periodo (T).
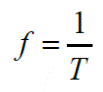
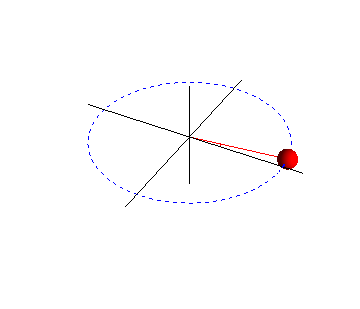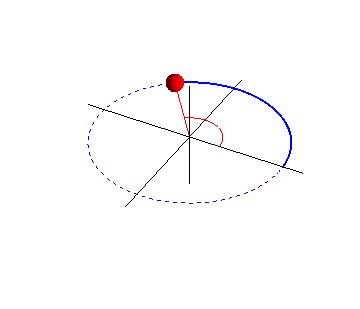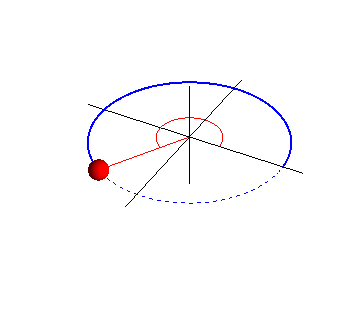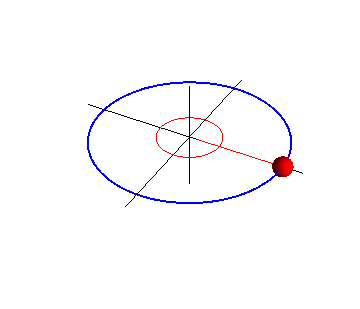
Una vez situado el origen O describimos el movimiento circular mediante las siguientes magnitudes angulares.
POSICIÓN ANGULAR (θ)
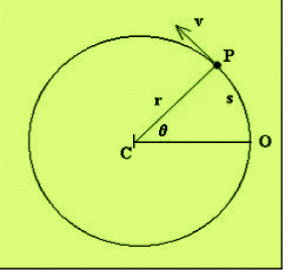
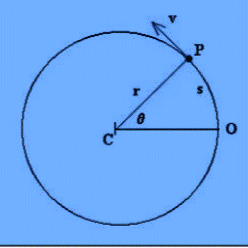 Podemos imaginar, como
ejemplo, que se tiene una piedra amarrada a una cuerda y la
movemos en círculos de radio r. En un instante de tiempo t el
móvil (en nuestro caso la piedra) se encuentra en el punto P.
Su posición angular (lo que la piedra ha recorrido en la
circunferencia) viene dada por el ángulo θ, formado por el
punto P, el centro de la circunferencia C y el origen O (desde
donde empezó a girar la piedra).
Podemos imaginar, como
ejemplo, que se tiene una piedra amarrada a una cuerda y la
movemos en círculos de radio r. En un instante de tiempo t el
móvil (en nuestro caso la piedra) se encuentra en el punto P.
Su posición angular (lo que la piedra ha recorrido en la
circunferencia) viene dada por el ángulo θ, formado por el
punto P, el centro de la circunferencia C y el origen O (desde
donde empezó a girar la piedra).
RAPIDEZ ANGULAR (ω) Y VELOCIDAD ANGULAR
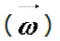
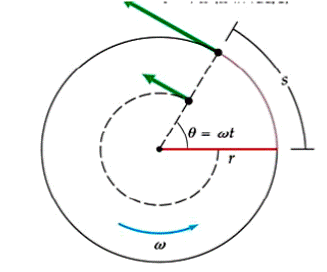 Cuando un objeto se mueve
en una circunferencia recorre un ángulo.
Cuando un objeto se mueve
en una circunferencia recorre un ángulo.
Se ha definido la rapidez angular como el ángulo recorrido (θ) dividido por unidad de tiempo, segundos.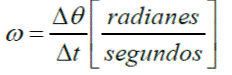
El resultado se da en radianes por cada segundo.
En forma simplificada:
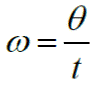
Donde:
ω = Rapidez angular en rad/s
θ = desplazamiento angular en rad.
t = tiempo en segundos en que se efectuó el desplazamiento angular.
La rapidez angular también se puede determinar si sabemos el tiempo que tarda en dar una vuelta completa o periodo (T):
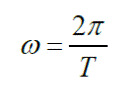
como:
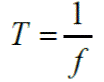
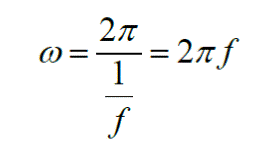
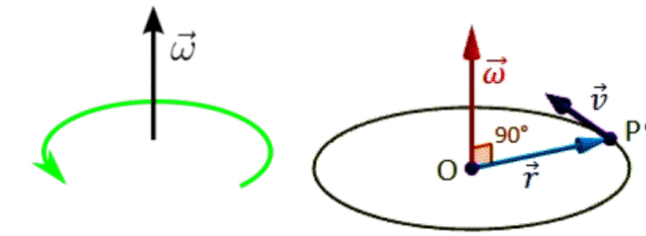
La rapidez angular ω, así definida, corresponde al módulo o intensidad de la rapidez angular, ya que la velocidad angular
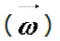 es una magnitud vectorial, que es un
vector perpendicular al plano de la
circunferencia.
es una magnitud vectorial, que es un
vector perpendicular al plano de la
circunferencia.
La velocidad angular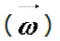 es un vector perpendicular desde el
centro de la circunferencia, con un sentido determinado
convencionalmente por la regla de la mano derecha o regla del
tirabuzón. Al empuñar la mano, el pulgar indica el sentido de
la velocidad angular y el resto de los dedos indican el sentido
de rotación.
es un vector perpendicular desde el
centro de la circunferencia, con un sentido determinado
convencionalmente por la regla de la mano derecha o regla del
tirabuzón. Al empuñar la mano, el pulgar indica el sentido de
la velocidad angular y el resto de los dedos indican el sentido
de rotación.


Aquí debemos señalar que una misma rapidez angular se puede expresar de varias maneras diferentes.
Por ejemplo, para las lavadoras automáticas o para los motores de los autos se usan las revoluciones por minuto (rpm). También a veces se usan las rps (revoluciones por segundo).
También se usan los grados por segundo y los radianes por segundo.
Por ejemplo, al transformar una rapidez de 60 rpm a frecuencia se obtiene: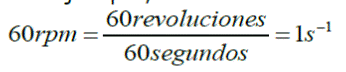
RAPIDEZ LINEAL (v)
 Es la razón entre el arco
descrito por el cuerpo y el tiempo empleado en
describirlo
Es la razón entre el arco
descrito por el cuerpo y el tiempo empleado en
describirlo
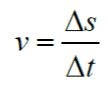
Si el radio describe ángulos iguales en tiempos iguales, el movimiento es circunferencial uniforme.
La distancia recorrida será un arco de la circunferencia o un determinado número de circunferencias, de modo que la rapidez media estará dada por:
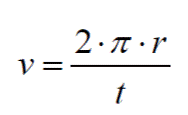
 Donde r es el radio, t el
tiempo empleado y 2⋅π⋅r la
distancia recorrida.
Donde r es el radio, t el
tiempo empleado y 2⋅π⋅r la
distancia recorrida.
Como en cada punto de la trayectoria, el movimiento cambia de dirección, resulta que la rapidez lineal corresponde solo al módulo del vector velocidad correspondiente.
El vector velocidad es tangente a cada punto de la circunferencia. La velocidad lineal o velocidad circunferencial se conoce también como velocidad tangencial
RELACIÓN ENTRE LA RAPIDEZ LINEAL O TANGENCIAL Y LA ANGULAR
Al dar una revolución completa, el camino recorrido corresponderá al arco completo (perímetro de la circunferencia) P = 2π r y el tiempo corresponderá al periodo (T)
Como: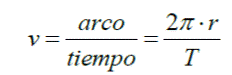
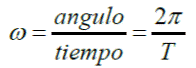
Entonces: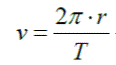
Por otra parte,
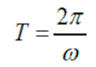
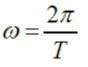
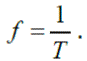
Finalmente: V=w R
Otra forma:
Al dividir la igualdad
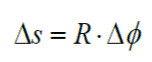
por el lapso Δt transcurrido resulta:
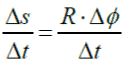
El primer miembro corresponde a la rapidez lineal o tangencial del movimiento, luego las rapideces lineal y angular están relacionadas por: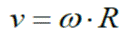
Esto significa que en un movimiento circunferencial, a mayor distancia al centro de la circunferencia mayor es la rapidez tangencial v, esto lo vemos ilustrado en un desfile, cuando la formación debe experimentar un giro o doblar en una esquina, con el objeto de no romper la formación (ω constante); los que se encuentran en el centro del giro prácticamente no deben moverse, en cambio los del extremo opuesto (mayor radio) deben dar grandes zancadas.
La aceleración en los movimientos curvilíneos
En los movimientos curvilíneos o circulares la dirección cambia a cada instante. Y debemos recordar que la velocidad considerada como vector v podrá variar (acelerar o decelerar) cuando varíe sólo su dirección, sólo su módulo o, en el caso más general, cuando varíen ambos.
La aceleración asociada a los cambios en dirección
En razón de la aseveración anterior, y desde un punto de vista sectorial (distancia), un movimiento circular uniforme es también un movimiento acelerado, aun cuando el móvil recorra la trayectoria a ritmo constante.
La dirección del vector velocidad, que es tangente a la trayectoria, va cambiando a lo largo del movimiento, y esta variación de v que afecta sólo a su dirección da lugar a una aceleración, llamada aceleración centrípeta.
ACELERACIÓN CENTRÍPETA
Cuando un móvil o la partícula realiza un movimiento circular uniforme, es lógico pensar que en cada punto el valor numérico de la velocidad (su módulo) es el mismo, en cambio es fácil darse cuenta de que la dirección del vector velocidad va cambiando a cada instante.
La variación de dirección del vector lineal origina una aceleración que llamaremos aceleración centrípeta. Esta aceleración tiene la dirección del radio y apunta siempre hacia el centro de la circunferencia.
Como deberíamos saber, cuando hay un cambio en alguno de los componentes del vector velocidad tiene que haber una aceleración. En el caso del movimiento circular esaaceleración se llama centrípeta, y lo que la provoca es el cambio de dirección del vector velocidad angular.
Veamos el dibujo: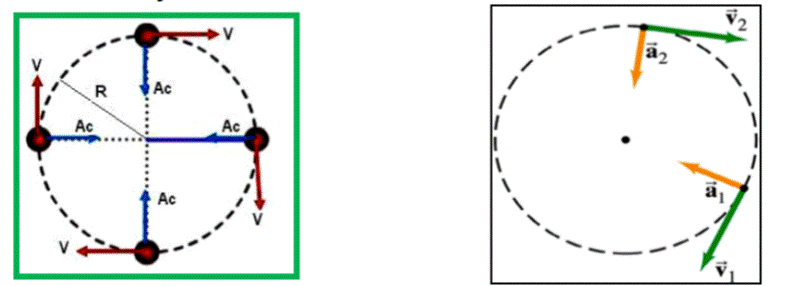
El vector velocidad tangencial cambia de dirección y eso provoca la aparición de una aceleración que se llama aceleración centrípeta, que apunta siempre hacia el centro.
La aceleración centrípeta se calcula por:
FUERZA CENTRÍPETA
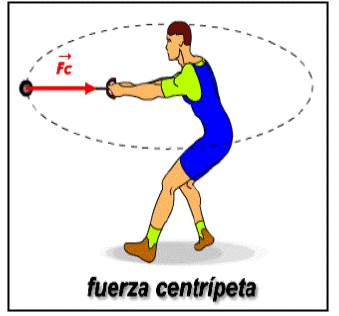 Según el principio de
masa formulado por Newton, para que un cuerpo posea una
aceleración, debe permanentemente actuar sobre él una fuerza.
Por lo tanto, sobre un cuerpo que gira en torno a una
circunferencia, debe actuar una fuerza hacia el centro de giro,
llamada fuerza centrípeta =
Según el principio de
masa formulado por Newton, para que un cuerpo posea una
aceleración, debe permanentemente actuar sobre él una fuerza.
Por lo tanto, sobre un cuerpo que gira en torno a una
circunferencia, debe actuar una fuerza hacia el centro de giro,
llamada fuerza centrípeta = 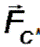 , la que obliga al cuerpo a mantenerse
sobre la trayectoria circular, provocando una aceleración
centrípeta.
, la que obliga al cuerpo a mantenerse
sobre la trayectoria circular, provocando una aceleración
centrípeta.
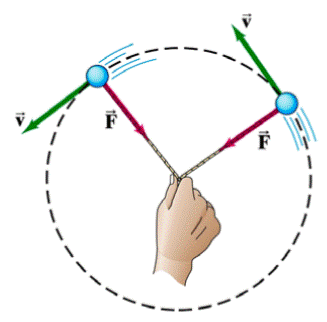
Tal fuerza tendrá la misma dirección y el mismo sentido que la aceleración centrípeta, o sea, apuntará hacia el centro de la curva. Por este motivo, recibe el nombre de fuerza centrípeta. Siendo m la masa del cuerpo en movimiento circular de radio r, podemos escribir:
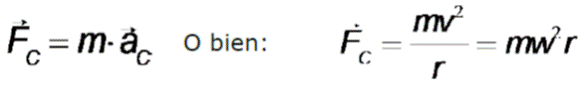
La fuerza centrípeta permite que el cuerpo se mantenga en la órbita circular, si esta no existiese, el cuerpo seguiría una trayectoria rectilínea.Vuelta a una curva plana
Un automóvil deportivo del ejemplo va por una curva sin peralte de radio R. Si el coeficiente de fricción estática entre los neumáticos y la carretera es μs, ¿cuál es la rapidez máxima con que el conductor puede tomarse la curva sin derrapar?
La aceleración del automóvil al tomar la curva tiene magnitud a= v2/R, así que la rapidez máxima vmáx (nuestra incógnita) corresponde a la aceleración máxima, y a la fuerza horizontal máxima sobre el auto hacia el centro del camino circular. La única fuerza horizontal que actúa sobre el auto es la fuerza de fricción ejercida por la carretera. Por lo tanto, tendremos que usar la segunda ley de Newton y la fuerza de fricción.
La fuerza de fricción debe apuntar hacia el centro de la trayectoria circular para causar la aceleración radial. Puesto que el auto no se mueve en la dirección radial (es decir, no se desliza hacia el centro del círculo ni en la dirección opuesta), la fuerza de fricción es estática con una magnitud máxima fmáx =μsN
La aceleración hacia el centro de la trayectoria circular es a=v2/R y no hay aceleración vertical. Entonces:
Así que la rapidez máxima es
 En las curvas de los
caminos, en las que los vehículos se desplazan con cierta
velocidad, existe una inclinación llamada peralte, la que
impide que el vehículo desbarranque. Esto se debe a que la
inclinación del vehículo genera una fuerza, componente de su
peso, hacia el centro de giro.
En las curvas de los
caminos, en las que los vehículos se desplazan con cierta
velocidad, existe una inclinación llamada peralte, la que
impide que el vehículo desbarranque. Esto se debe a que la
inclinación del vehículo genera una fuerza, componente de su
peso, hacia el centro de giro.
Un ciclista, al girar en una curva, inclina su cuerpo hacia el centro de rotación para no caer; de manera similar, un avión, también se inclina al momento de girar, para generar la fuerza que le permita efectuar el giro.El efecto de la fuerza centrípeta se aplica en el proceso de entrenamiento de pilotos de guerra. Cuando el avión experimenta un giro a gran velocidad, el piloto queda sometido a una fuerza muy intensa, lo que genera efectos significativos sobre su cuerpo, especialmente en el sistema circulatorio, por lo que es necesario estar en óptimas condiciones físicas para desarrollar esta actividad.
En los laboratorios, se utilizan ultra centrifugas para acelerar procesos de sedimentación, lo que permite, por ejemplo, separar componentes de la sangre; de igual forma, las descremadoras, permiten separar los componentes por sus densidades, ya que la crema, al ser menos densa, tiende a situarse en torno al eje de rotación, y los elementos más pesados, en las paredes.
EFECTO DE FUERZA CENTRÍFUGA
Cuando viajas en un automóvil, muchos de los movimientos que realiza tu cuerpo obedecen a la inercia del movimiento. Por ejemplo, el moverte hacia delante cuando el vehículo frena o hacia atrás cuando acelera. La inercia es la tendencia de los cuerpos a permanecer en el estado de movimiento en que se encuentran. Es decir, los movimientos descritos al viajar en un automóvil no se producen por la acción de una fuerza hacia delante o hacia atrás, sino por el efecto de la inercia.
A veces se le atribuye al movimiento circular uniforme una fuerza dirigida hacia fuera llamada fuerza centrífuga. Es cierto que cuando vamos en un vehículo y éste dobla hacia la izquierda, nuestro cuerpo tiende a irse hacia la derecha. Sin embargo, eso no se debe a ninguna fuerza, sino a la inercia de nuestro cuerpo que tiende a seguir en la trayectoria rectilínea que traía.
Por lo tanto, el efecto fuerza centrífuga no se atribuye a una fuerza real, sino que a la inercia que hace que un cuerpo en movimiento tienda a desplazarse a lo largo de la trayectoria en línea recta.
TRANSMISIÓN DE MOVIMIENTO
1) Ruedas tangenciales: El movimiento circunferencial se puede transmitir de una rueda a otra, por medio de correas de transmisión, o por medio de ruedas dentadas.Supongamos dos ruedas de radio diferente, unidas por una cuerda inextensible, como muestra la figura. Por efecto de la comunicación de la cuerda, se cumple que:
y como vRω=⋅ Entonces: 1122rrωω⋅=⋅ Como 2fωπ=⋅ , se cumple también que 2π112frπ⋅⋅=22fr⋅⋅ 1122frfr⋅=⋅ Lo anterior nos indica que la frecuencia entre ruedas ligadas entre sí es inversamente proporcional a sus respectivos radios. Este mecanismo es de gran utilidad, pues podemos modificar la frecuencia, en función a los radios del sistema de transmisión. En el caso de las bicicletas existen, sistemas de transmisión a través de ruedas dentadas, las que están comunicadas por medio de cadenas.
2) Ruedas concéntricas: Si dos o más partículas giran en base a un mismo centro, sus velocidades angulares serán iguales.
como:
entonces se cumple:
-
-
-
Recurso
-
-
-
Cuestionario
-
Cuestionario
-
Cuestionario
-