Diagrama de temas
-
-
Foro
-
-
-
En la naturaleza nos encontramos con el concepto de fuerza, se puede señalar que las fuerzas se manifiestan en numerosos ejemplos de la vida diaria. Así al golpear un balón con el pie o levantar un objeto de mucha masa o golpear una pelota de tenis se aplica una fuerza. Es decir, Fuerza es toda causa capaz de modificar el estado de reposo o de movimiento de un cuerpo o producirle una deformación Estas fuerzas se identifican ya que producen efectos observables sobre los objetos.




Por ejemplo, una fuerza puede:




De estas experiencias se deduce que, para que exista una fuerza tienen que interaccionar dos objetos. Una misma fuerza puede ocasionar diversos efectos sobre un mismo objeto. Así, un balón de fútbol golpeado con el pie puede rodar sobre la hierba o salir impulsado hacia arriba. También, se puede parar o modificar su trayectoria y si se pisa, se deforma.
Los objetos pueden interaccionar de dos formas: entrando en contacto o estando a cierta distancia entre sí. Por tanto, las fuerzas se clasifican en: fuerzas por contacto y fuerzas a distancia.
Fuerzas por contacto: En la vida diaria se manifiestan fuerzas por contacto como por ejemplo contacto entre cuerpos, resortes, objetos apoyados en superficies, estructuras, entre otros.


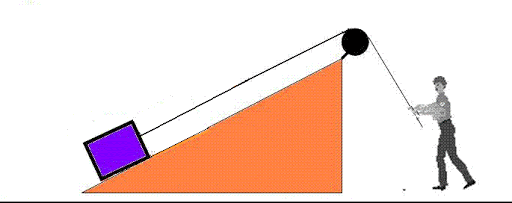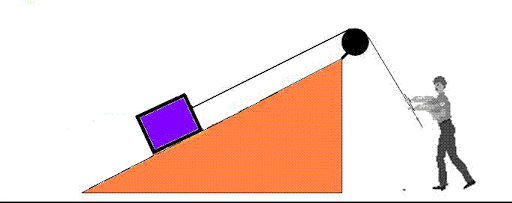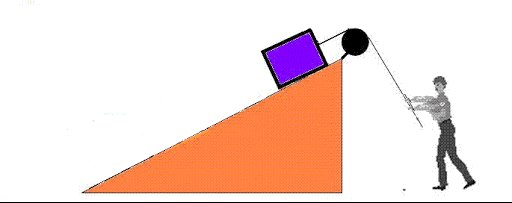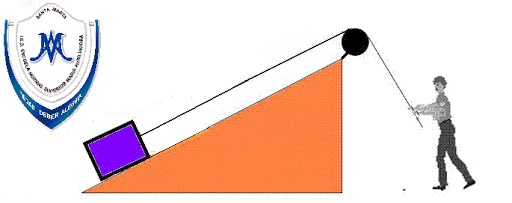

Fuerzas a distancia:
Las fuerzas a distancia son todas aquellas que se ejercen sin necesidad de entrar en contacto con respecto al cuerpo que genera dicha fuerza y el que la recibe, una característica de este tipo de fuerzas suelen crear campos de fuerza. Este concepto está incluido dentro del campo de la física, tal vez uno de los ejemplos más extremos de este tipo de fuerza es el de las nucleares y en este caso las partículas generan cohesión en el núcleo del átomo, por otro lado un ejemplo más común que se puede ver en diferentes momentos y situaciones de la vida cotidiana son los imanes (cuando están separados) los cuales están presentes en casi todos los electrodomésticos y dispositivos tecnológicos que usamos. También en la atracción entre el planeta Tierra y la luna.
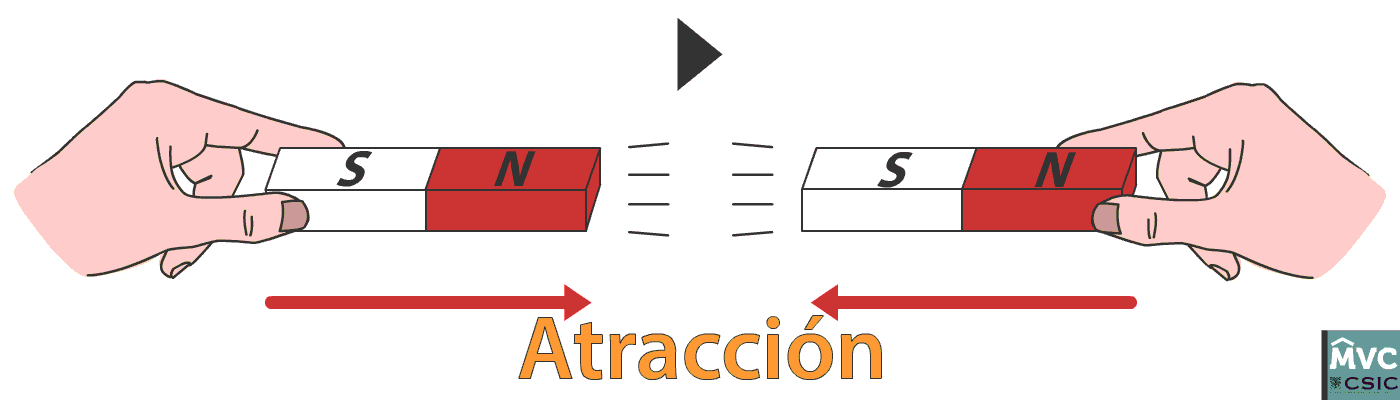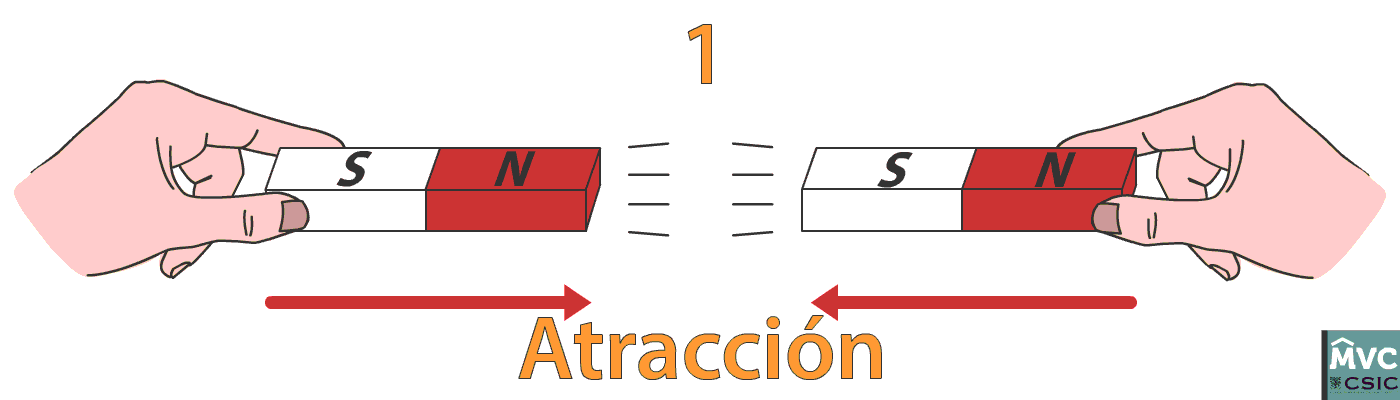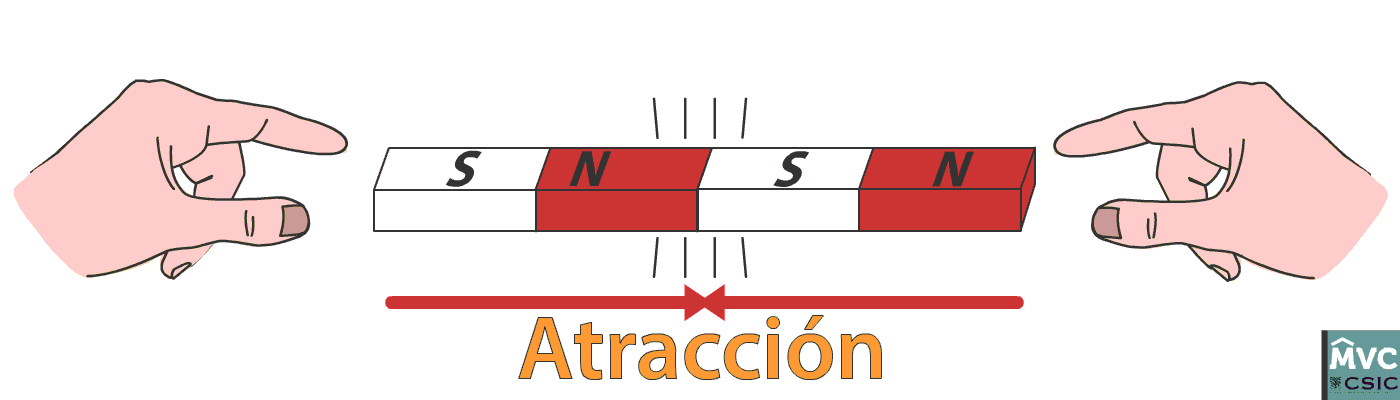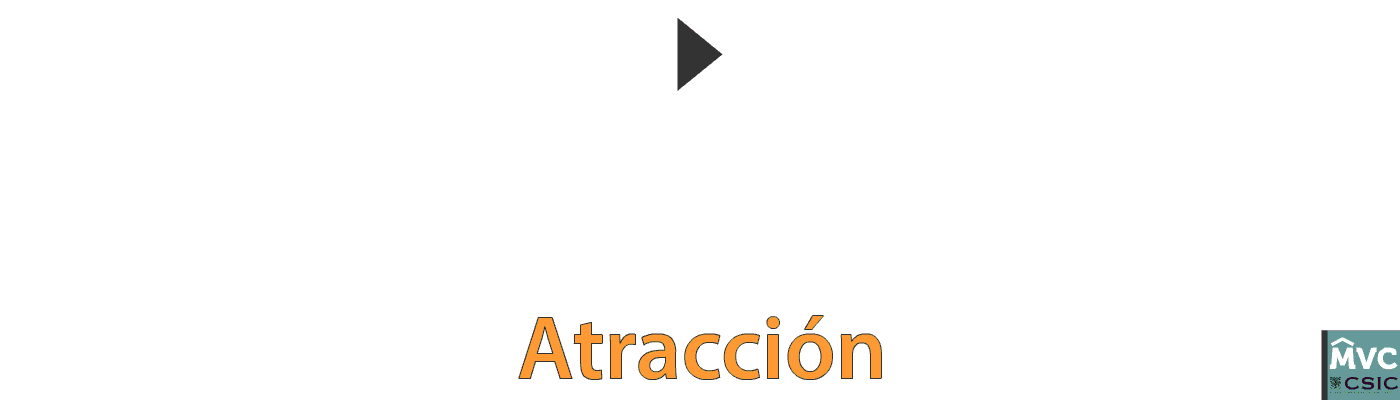


FUERZA, UNA MAGNITUD VECTORIAL
En Física, para comprender mejor los fenómenos de la naturaleza, se realizan mediciones de dichos fenómenos. En la mediciones se pueden encontrar dos tipos de magnitudes: Escalares y vectoriales
Magnitudes escalares: Las magnitudes escalares quedan bien definidas únicamente con su intensidad, un número que representa una determinada cantidad. Es decir, aquellas que quedan definidas exclusivamente por un módulo, es decir, por un número acompañado de una unidad de medida. Es el caso de masa, tiempo, temperatura, distancia. Por ejemplo, 5 kg, 6,9 segundos, 400 °C y 8 km, respectivamente.
Por lo tanto son aquellas que para quedar bien definidas se requiere su intensidad (valor numérico) y unidad. Ejemplo el tiempo: 20 segundos, estas se abrevian con una letra: t = 20 s

Magnitudes vectoriales: En muchos casos las magnitudes escalares no dan información completa. Para localizar con precisión la posición de los objetos, respecto de un sistema de referencia, hay que expresar además del valor numérico y la unidad de esa distancia, la dirección y el sentido en que se encuentran. Esa información la indican las magnitudes vectoriales. Por ejemplo una fuerza de determinado valor puede estar aplicada sobre un cuerpo en diferentes sentidos y direcciones.
Por lo tanto son aquellas que para quedar bien definidas se requiere su intensidad (valor numérico), unidad y además su dirección-sentido. Ejemplo la fuerza: 50 Newton hacia el norte, estas se abrevian con una letra y sobre ella una flecha:


Tenemos entonces las magnitudes vectoriales que, como su nombre lo indica, se representan mediante vectores, es decir que además de un módulo (o valor absoluto) tienen una dirección y un sentido. La dirección es la recta a la que pertenece el segmento de la flecha, y el sentido viene indicado por la punta de la flecha.
Los vectores se abrevian con una letra y sobre ella se coloca una flecha, ejemplo: Fuerza F= 6 N

Ejemplos de magnitudes vectoriales son la velocidad y la fuerza. Ejemplo un vehículo se mueve con una velocidad de 50 km/h, en la carretera, hacia el Sur de Chile.

Definimos una fuerza como toda causa capaz de modificar el estado de reposo o de movimiento de un cuerpo, o de producir una deformación en él. Una fuerza es la interacción de un cuerpo con algo externo a él y es una magnitud vectorial caracterizada por poseer módulo, dirección, sentido y punto de aplicación o punto origen.
La unidad de medida en el Sistema Internacional de Unidades (S.I) es el Newton (N). En honor a Isaac Newton, un físico que realizo estudios sobre las fuerzas.
Las acciones que se ejercen sobre un cuerpo, además de ser más o menos intensas (valor o módulo de la fuerza) son ejercidas según una dirección: paralelamente al plano, perpendicularmente a éste, formando un ángulo de 30… y en determinado sentido: hacia la derecha, hacia la izquierda, hacia arriba, hacia abajo. Por estas razones las fuerzas para estar correctamente definidas tienen que darnos información sobre su valor (módulo), dirección y sentido. Por eso se representan por flechas (vectores)
¿Qué ocurre si sobre un cuerpo actúa más de una fuerza?
Podemos obtener sólo una que produzca el mismo efecto que todas actuando a la vez. Esto se consigue sumando las fuerzas actuantes. ¿Cómo?
• Fuerzas con la misma dirección y sentido: se suman los módulos. La fuerza resultante tiene la misma dirección y sentido y su módulo es la suma de las actuantes.
Ejemplo 1:
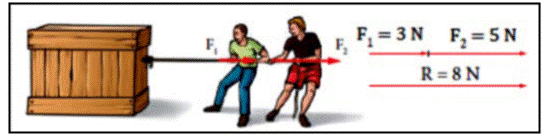
— Modulo: la suma de los módulos de las fuerzas componentes.
R = F1 + F2
— Dirección: la misma que las fuerzas componentes.
— Sentido: el mismo que las fuerzas componentes.
Ejemplo 2:

• Fuerzas de la misma dirección y sentido contrario: se restan los módulos. La fuerza resultante tiene la misma dirección y su sentido viene dado por el signo resultante: si es positivo apunta en el sentido que se ha considerado como tal y si es negativo en sentido contrario.
Ejemplo 3:
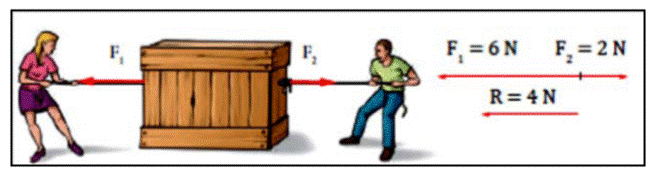
— Modulo: la diferencia, en valor absoluto, entre los módulos de las fuerzas componentes.
R = F1 – F2
— Dirección: la misma que las fuerzas componentes.
— Sentido: el mismo que la fuerza de mayor módulo.
Ejemplo 4
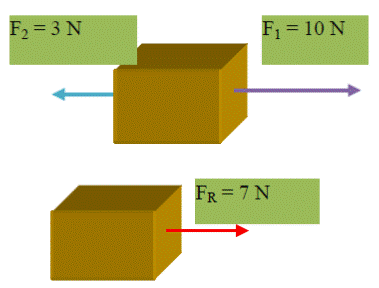
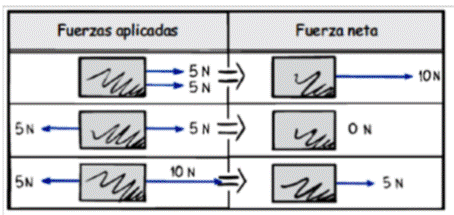
FUERZA: EL ORIGEN, LA CAUSA DEL MOVIMIENTO


El inglés Isaac Newton formuló y desarrolló una potente teoría acerca del movimiento, según la cual las fuerzas que actúan sobre un cuerpo producen un cambio en el movimiento de dicho cuerpo.
Newton, uno de los más grandes físicos de la historia, formuló tres leyes, enunciadas en 1687 y hacen referencia al movimiento de los cuerpos. La primera es la ley de inercia, la segunda es la relación entre fuerza y aceleración, y por último la ley de acción y reacción. Para los fenómenos de la vida diaria, esas tres leyes del movimiento son la piedra angular de la dinámica.
LEYES DE NEWTON

La Dinámica comprende tres leyes que generalmente reciben el nombre de Leyes del movimiento de Newton:
1. Ley de Inercia
2. Ley de la Fuerza o Ley de la Masa
3. Ley de Acción y Reacción
Aunque estas leyes son llamadas comúnmente Leyes de Newton, por haber sido este físico quien primero las enunció en forma correcta y la aplicó a casos concretos. Debe tenerse presente que el descubridor de la Ley de Inercia fue el físico italiano Galileo Galilei, y la Ley de la Fuerza era conocida por el astrónomo alemán Johannes Kepler.
PRIMERA LEY DE NEWTON O PRINCIPIO DE INERCIA:
La idea aristotélica de que un objeto en movimiento debe estar impulsado por una fuerza continua fue demolida por Galileo, quien dijo que en ausencia de una fuerza, un objeto en movimiento continuará moviéndose. La tendencia de las cosas a resistir cambios en su movimiento fue lo que Galileo llamó inercia. Newton refinó esta idea de Galileo, y formuló su primera ley, que bien se llama ley de la inercia. En los Principia de Newton (traducido del original en latín)

Todo objeto continúa en su estado de reposo o de movimiento uniforme en línea recta, a menos que sea obligado a cambiar ese estado por fuerzas que actúen sobre él.
La palabra clave de esta ley es continúa: un objeto continúa haciendo lo que haga a menos que sobre él actúe una fuerza. Si está en reposo continúa en un estado de reposo. Esto se demuestra muy bien cuando un mantel se retira con habilidad por debajo de una vajilla colocada sobre una mesa y los platos quedan en su estado inicial de reposo. La propiedad de los objetos de resistir cambios en su movimiento se le llama inercia.
Newton complementó los trabajos realizados por Galileo en lo referente a la relación entre fuerza y movimiento. Galileo trabajó sobre el movimiento que realizaban los cuerpos en una superficie horizontal, una vez se les daba cierto impulso. Newton repitió dichos experimentos y descubre que cuanto más lisas son las superficies, tanto más lejos se deslizará el cuerpo antes de llegar al reposo (V = 0), una vez que se hubiese dado el mismo impulso. O sea, cuanto más lisas son las dos superficie en contacto tanto menos se desacelera el objeto y tanto más débil es la fuerza de fricción que actúa sobre él.
La primera ley de Newton o Principio de Inercia de Galileo como también se le conoce es un enunciado de un experimento idealizado (Porque no existe roce).

Si está en reposo, continúa en ese estado. Si se está moviendo, continúa haciéndolo sin cambiar de dirección ni de rapidez. La ley establece que un cuerpo no se acelera por sí mismo; la aceleración debe ser impuesta contra la tendencia de un cuerpo a conservar su estado de movimiento. La tendencia de un cuerpo a oponerse a un cambio en su movimiento, es lo que Galileo denominó Inercia.
La inercia de la materia en “estado de reposo” es evidente, pues un objeto en estado de reposo respecto a un marco de referencia, no puede ponerse por sí mismo en estado de movimiento.
Esto demuestra que todos los cuerpos que están en movimiento tienden a seguir en movimiento; los cuerpos que están en reposo, tienden a seguir en reposo. Esta es la primera Ley de Newton, que se enuncia así:
“Todo cuerpo permanece en reposo o se desplaza con movimiento rectilíneo uniforme, siempre que no actúe sobre él una fuerza exterior que cambie su estado”
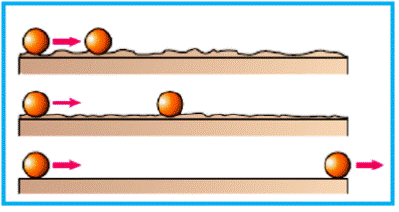
En ausencia de la fricción la pelota de la figura no se detendrá nunca.
Aunque Galileo fue quien introdujo el concepto de inercia, fue Newton quien valoró su importancia. La ley de la inercia define el movimiento natural e indica que clases de movimiento son el resultado de las fuerzas aplicadas.
Todo cuerpo posee inercia. Depende de la cantidad de materia en la sustancia de un cuerpo; a mayor cantidad de materia, mayor inercia. Al hablar de cuánta materia tiene un cuerpo, se emplea el término masa. La masa es una medida de la inercia de un cuerpo.


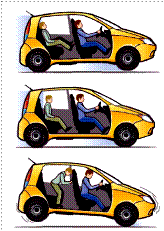
Cuando un vehículo arranca bruscamente las personas se mueven hacia atrás. Ello se debe a que tienden a conservar su estado de movimiento, que era estar en reposo.
De la misma forma, si el vehículo frena con brusquedad, los pasajeros se mueven hacia adelante, porque tienden a continuar con su estado de movimiento, que era de velocidad constante.

SEGUNDA LEY DE NEWTON O PRINCIPIO DE MASA
La primera ley de Newton nos dice que le pasa a un cuerpo si sobre el no actúa ninguna fuerza. Ahora bien, ¿qué le pasará a un cuerpo si existe una fuerza resultante que actúa sobre él? La segunda ley de Newton resuelve esta cuestión.
Una vez que se conocen las características del movimiento cuando no actúa una fuerza o cuando la fuerza resultante es cero, las preguntas que surgen naturalmente son: ¿Qué pasa si la suma de las fuerzas no se anula? ¿Cómo se mueve un sistema sujeto a la acción de una sola fuerza o de una fuerza resultante diferente de cero?
La observación, los experimentos y la reflexión llevaron a Newton a concluir que en estas condiciones la velocidad de un cuerpo no se mantiene constante. Si está en reposo, comenzará a moverse y si está en movimiento, su rapidez o la dirección y sentido de su movimiento cambiará; en pocas palabras, el cuerpo adquiere una aceleración.
Se habla de aceleración cuando un cuerpo cambia la velocidad en un determinado tiempo.
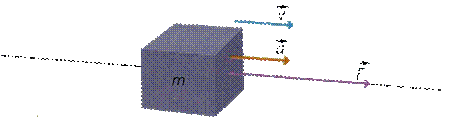
Experimentalmente se comprueba que si actúa una fuerza sobre un objeto en reposo, entonces se mueve siguiendo la misma dirección y sentido que los de la fuerza aplicada y su velocidad aumenta. Si se mantienen constantes el módulo, la dirección y el sentido de la fuerza aplicada, entonces el objeto se traslada en línea recta aumentando su velocidad de forma constante, o lo que es lo mismo, el objeto se desplaza siguiendo un movimiento rectilíneo con aceleración constante.
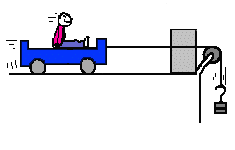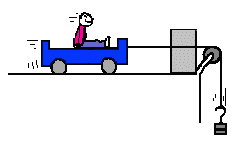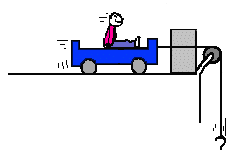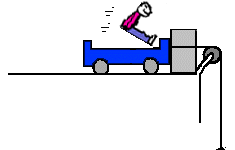
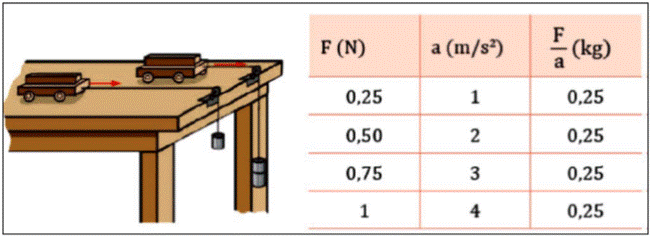
Ejemplo: Se aplica una fuerza F a un carrito en reposo. Este adquiere una aceleración a e inicia un MRUA. Fíjate en que la aceleración que adquiere depende de la fuerza aplicada.
La razón entre la fuerza resultante que actúa sobre un cuerpo y la aceleración que adquiere el cuerpo como consecuencia de dicha fuerza es una constante igual a la masa del cuerpo.
La constatación de este hecho constituye el enunciado de la segunda ley de Newton.
Newton determinó que la aceleración que adquiere un cuerpo depende tanto de la magnitud, la dirección y el sentido de la fuerza resultante que actúa sobre él, como de la masa del objeto. La fuerza resultante y la masa son las únicas variables involucradas.
La aceleración es directamente proporcional a la magnitud de la fuerza resultante. Así, si se duplica la fuerza, la aceleración se duplica; si se triplica la fuerza, se triplica la aceleración.
Se concluye entonces que:
La fuerza F que actúa sobre un cuerpo es directamente proporcional a la aceleración que produce.
Por otro lado, la aceleración es inversamente proporcional a la masa del cuerpo que se acelera. Esto es, a mayor masa, menor aceleración. Si aplicas la misma fuerza sobre dos cajas, una con el doble de la masa que otra, la aceleración de la de mayor masa será sólo la mitad. La masa resulta ser una medida de la inercia del objeto o de su resistencia a ser acelerado.

Se concluye entonces que:

La Segunda Ley de Newton resume estas observaciones.
El módulo de la fuerza que actúa sobre un objeto es proporcional a la aceleración que le produce, siendo la constante de proporcionalidad una característica del objeto, y coincide con su masa.
La masa es una magnitud escalar y la fuerza y la aceleración son magnitudes vectoriales que tienen la misma dirección y sentido. Por tanto, la expresión vectorial de la ecuación anterior es:
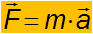
Por lo tanto la segunda Ley de Newton señala:

Unidades de Fuerza:
Al usar la Segunda Ley de Newton, F= m• a, debemos recordar que:
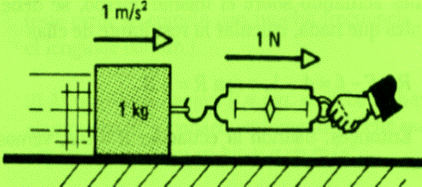
F (en Newton) = m (en kg) • a (en m/s2)
Es decir, 1 kg• m/s2 = 1 Newton
TERCERA LEY DE NEWTON O PRINCIPIO DE ACCIÓN-REACCIÓN
Cuando un cuerpo ejerce una fuerza sobre otro, ¿cómo responde este segundo cuerpo?
Para comprenderlo, observa estos ejemplos.
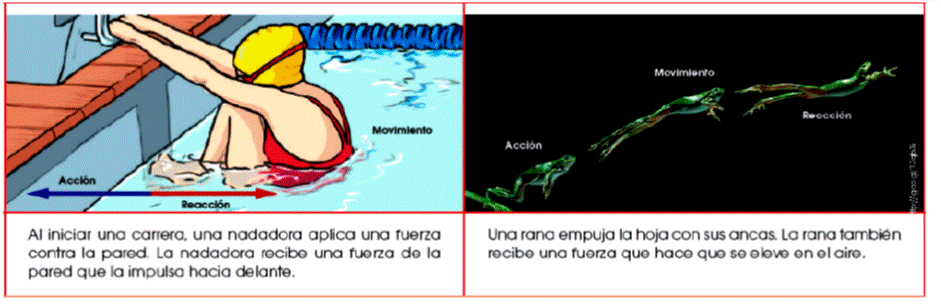

Los conocimientos sobre interacciones entre cuerpos son una buena base para estudiar la tercera ley de Newton. La acción de una fuerza sobre un cuerpo no se puede manifestar sin que haya otro cuerpo que la provoque. De esto se deduce que del resultado de una interacción aparecen dos fuerzas, es decir, que las fuerzas se presentan por pares, lo que hace imposible la existencia de una sola fuerza en la naturaleza.
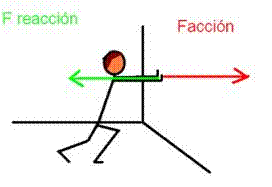
La acción de un objeto sobre otro está siempre acompañada por una reacción del segundo cuerpo sobre el primero. La tercera ley de Newton indica claramente como se relaciona las fuerzas en una interacción.
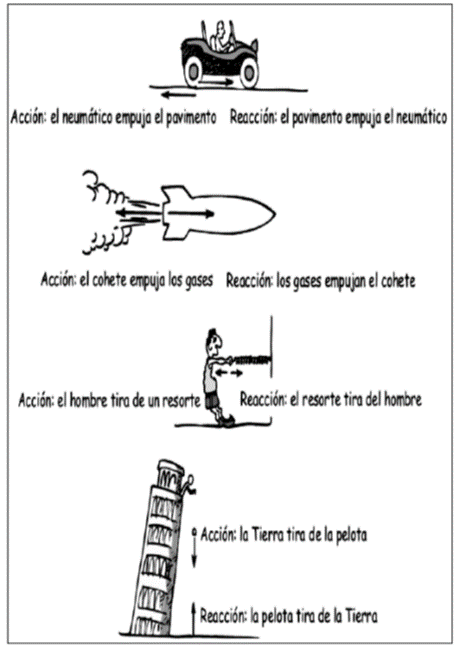
La tercera Ley del Movimiento de Newton es el principio de acción y reacción. Este postula que a cada acción corresponde una reacción igual y contraria. Es decir, si un cuerpo A ejerce una acción sobre un cuerpo B, el cuerpo B reacciona y ejerce una fuerza igual y contraria sobre el cuerpo A.
Los cohetes funcionan en base al mismo principio, ya que se aceleran al ejercer una gran fuerza sobre los gases que expulsan. Estos gases ejercen una fuerza igual y opuesta sobre el cohete, lo que finalmente lo hace avanzar.
La tercera ley de Newton se establece a menudo como sigue: “A toda acción siempre se opone una reacción igual.”
Es importante insistir que las fuerzas de acción y reacción actúan sobre diferentes cuerpos. Nunca actúan sobre el mismo cuerpo. Las fuerzas de acción y reacción constituyen un par de fuerzas.
Las fuerzas siempre ocurren en pares. Nunca existe una fuerza única en ninguna situación.

Por todas partes se observa el cumplimiento de la tercera ley de Newton. Un pez empuja el agua hacia atrás con sus aletas y el agua a su vez empuja al pez hacia delante. El viento empuja contra las ramas de un árbol con lo que generan silbidos.
Las fuerzas son interacciones entre cosas diferentes. Cada contacto requiere de por lo menos un dúo; no hay forma de que un cuerpo pueda ejercer una fuerza sobre nada.
Las fuerzas, siempre ocurren en pares, y cada miembro del par es opuesto al otro. Así, no se puede tocar sin ser tocado.
OBSERVACIONES:
- Para que se manifieste una fuerza tiene que haber más de un cuerpo como mínimo. Las fuerzas aparece de a pares.
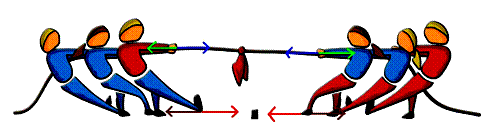
- La acción y reacción no se anulan porque no actúan en el mismo cuerpo.
- En la acción-reacción, las fuerzas son de igual magnitud y dirección, pero de sentido inverso.
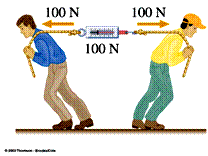
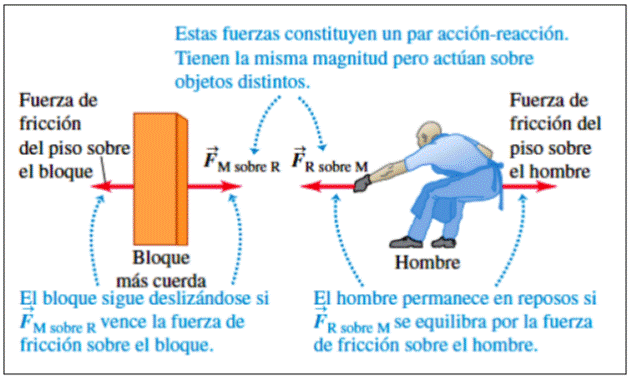
- La acción y reacción no necesariamente producen los mismos efectos.
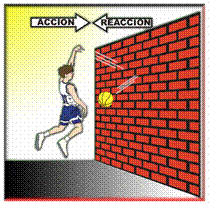

¿Cuál de los dos zumos
experimenta una mayor fuerza?
TIPOS DE FUERZAS
1.- Peso de un cuerpo:

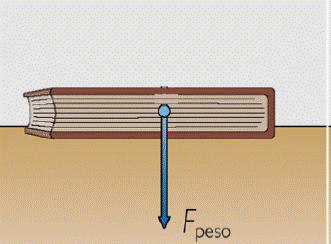
Es la fuerza gravitatoria con la cual un cuerpo celeste (en nuestro caso la Tierra) atrae a otro, relativamente cercano a él.
El peso en nuestro planeta es la fuerza con la que la Tierra atrae a dicho cuerpo. El peso es una magnitud vectorial, pues se trata de una fuerza.
El peso de un cuerpo es la fuerza que hace que éste caiga en las proximidades de la superficie de la Tierra, con la aceleración de la gravedad o gravitatoria “g”
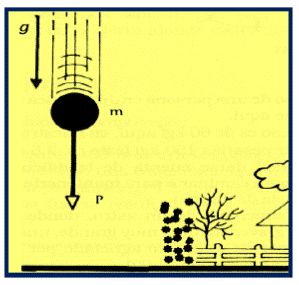
Entonces, si usamos la Segunda Ley de Newton,
F = m•a,
para determinar el peso tenemos:
P = m • g
“el peso de un cuerpo no es constante, pues "g" varía de un lugar a otro”
Variación del peso
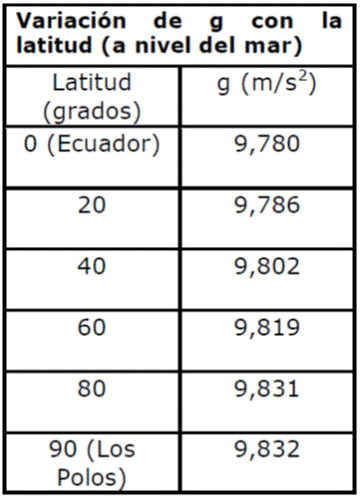
El valor de la aceleración de la gravedad “g” varía de un lugar a otro de la superficie de la Tierra.
Midiendo este valor, fue posible comprobar que “g” es mayor cerca de los polos que en las proximidades del Ecuador.
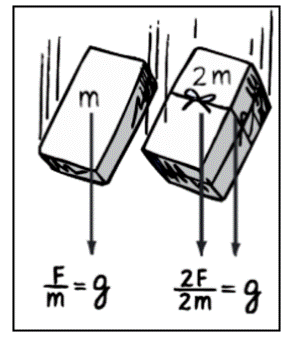
Por lo tanto, la ecuación P = m•g permite concluir que un cuerpo es más pesado cerca de los polos, y más ligero en las proximidades del Ecuador.
Se nota también que el valor de g decrece a medida que la altitud aumenta. Así, el peso de un cuerpo decrece a medida que aumenta la altitud del punto en donde se encuentra. En la ciudad de México (donde g = 9.78 m/s2), en Quito (en Ecuador), en La Paz (en Bolivia), etc., el valor del peso de un cuerpo, en virtud de la gran altitud de estas ciudades, es menor que al nivel del mar. Recuerda, sin embargo, que la masa del cuerpo tiene siempre el mismo valor en todos esos lugares.
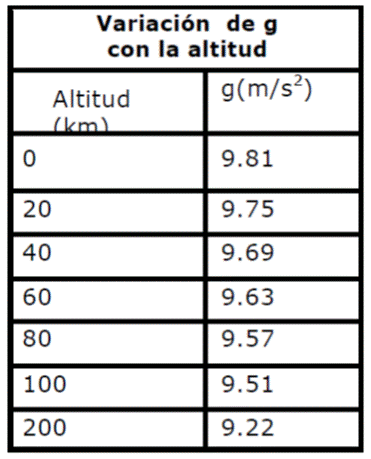
Cuando nos trasladamos a otro lugar, por ejemplo, a la Luna, a otros planetas, la aceleración de gravedad en estos lugares posee valores muy diferentes.
En la superficie de la Luna tenemos que g = 1.6 m/s2 (cerca de 6 veces menor que la de la Tierra). Por tanto, la fuerza con la que la Luna atrae un cuerpo, es decir, su peso en la Luna, es 6 veces menor que en la Tierra.
En el caso de la fuerza respecto al peso, una unidad muy usada todavía en la práctica es el kilogramo-fuerza, que se representa con el símbolo kgf.
El kilogramo-fuerza (Kgf) es la fuerza (peso) con que la Tierra atrae a 1 kilogramo de masa.
El kilogramo-fuerza no es unidad del Sistema Internacional, sino del sistema técnico, la unidad de fuerza se denomina Newton (símbolo: N) en honor al físico inglés Isaac Newton, que formuló leyes básicas de la Mecánica.
La relación entre estas dos unidades es la que sigue:
1 kgf = 9.8N.
O, aproximadamente, como usaremos, en este curso:
1kgf=10N

El aparato para medir una fuerza se denomina dinamómetro. Supongamos que una persona se sube a una balanza y ésta indica su peso: "60 kilos", como comúnmente se dice.
a) ¿Cuál es la manera correcta (en física) de expresar el peso de la persona?
La expresión popular "1 kilo" significa realmente 1 kgf, en este caso de medida de una fuerza. Por lo tanto, el peso de la persona, indicado por la báscula es de 60 kgf. Esto es, la Tierra atrae a la persona con una fuerza de 60 kgf.
b) ¿Cuál es el peso de esta persona en Newton? Como ya se dijo, vamos a considerar que 1 kgf = 10 N. En consecuencia, 60 kgf = 60 x 10 N=600 N
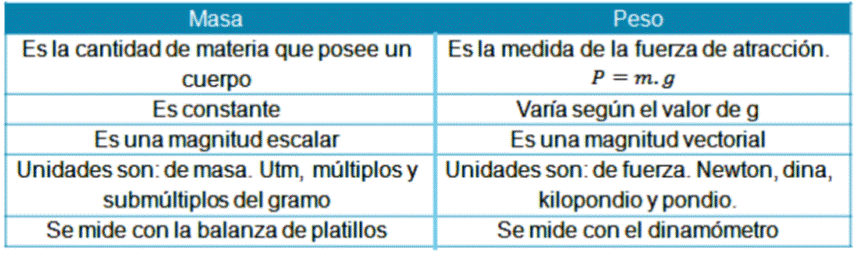
Tu peso es igual a la fuerza con que comprimes el suelo que te sostiene. Si el suelo acelera hacia arriba o hacia abajo, tu peso varía (aunque la fuerza gravitacional mg que actúa sobre ti permanezca invariable).


2.- Fuerza Normal:
La fuerza normal es aquella que ejerce una superficie como reacción a un cuerpo que ejerce una fuerza sobre ella.

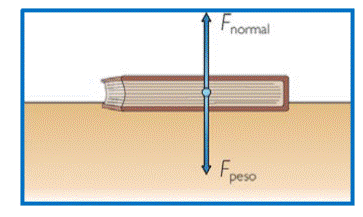
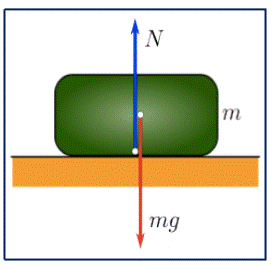
Si la superficie es horizontal y no hay otra fuerza actuando que la modifique (como por ejemplo la tensión de una cuerda hacia arriba), la fuerza normal es igual al peso pero en sentido contrario. En este caso una fuerza horizontal empujando el cuerpo no modifica la normal.
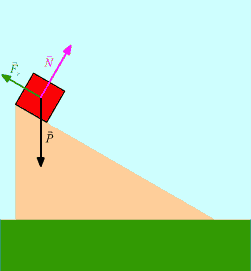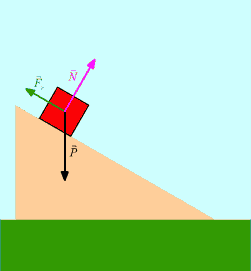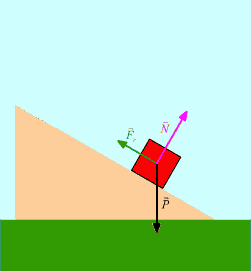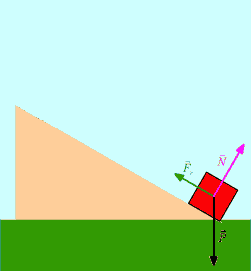
En un plano inclinado la normal es una proyección del peso. Generalizando, la fuerza normal es una fuerza de reacción de la superficie en sentido contrario a la fuerza ejercida sobre la misma.
La fuerza normal no es un par de reacción del peso, sino una reacción de la superficie a la fuerza que un cuerpo ejerce sobre ella.
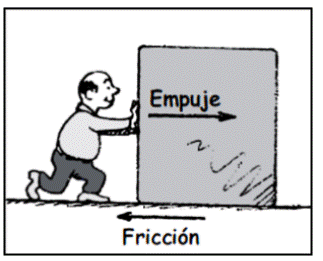
3.- Fuerza de rozamiento: es la fuerza que aparece en la superficie de contacto de los cuerpos, oponiéndose al movimiento de estos.
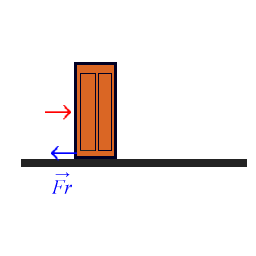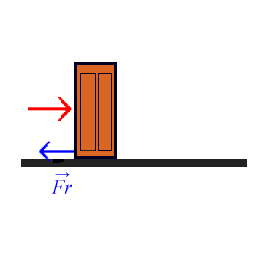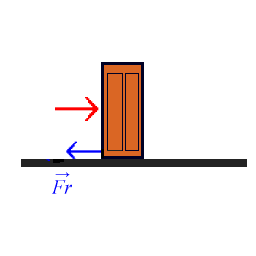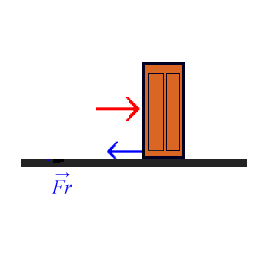
Las características de esta fuerza son las siguientes:
- Siempre es paralela a la superficie de contacto y tiene sentido contrario al movimiento que efectúa el cuerpo o al que se pretende provocar en él.
- Depende de la naturaleza y del estado de las superficies de contacto de los cuerpos, pero no del área de contacto. Cuanto más lisas sean estas superficies, menor será la fuerza de rozamiento.
- La fuerza de rozamiento que se opone al inicio de un movimiento es mayor que la fuerza que existe cuando el cuerpo ya está en movimiento.
- En el caso de un cuerpo en movimiento, es proporcional a la fuerza normal que se ejerce entre las dos superficies en contacto.
- La fuerza de rozamiento no depende del área de contacto de los cuerpos, esto se ha comprobado experimentalmente.

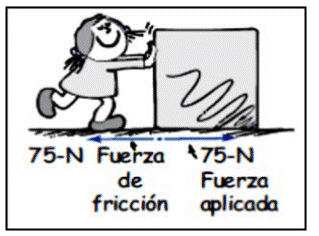
La fuerza de rozamiento es proporcional a la fuerza normal (N), la constante de proporcionalidad recibe el nombre de coeficiente de rozamiento, μ. En el caso de un cuerpo en reposo, la fuerza de rozamiento estática, compensa exactamente la fuerza aplicada en la dirección paralela a la superficie de contacto, hasta llegar a un valor máximo. Cuando se alcanza este valor, el cuerpo comienza a deslizarse, y actúa sobre él una fuerza de rozamiento cinética.
donde μ es lo que conocemos como coeficiente de rozamiento.
Hay dos coeficientes de rozamiento: el estático, μe, y el cinético, μc, siendo el primero mayor que el segundo: μe > μc
La fuerza de rozamiento dinámica es siempre algo menor que la fuerza estática máxima que puede ejercer la superficie. Esto explica el hecho de que necesitemos más fuerza para comenzar a arrastrar una caja que para mantener el movimiento una vez iniciado.
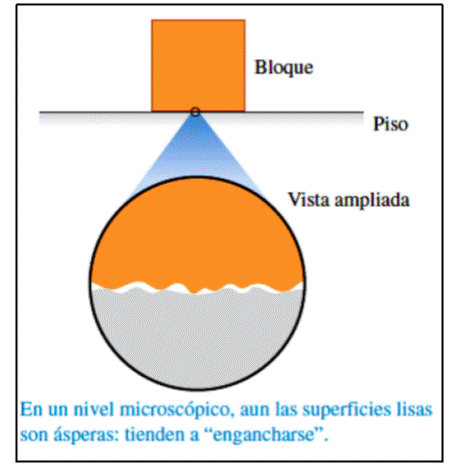
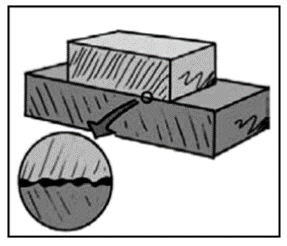
La fricción (rozamiento) resulta del mutuo contacto entre las irregularidades en la superficie de los objetos que se deslizan.
Hasta las superficies que parecen muy lisas tienen irregularidades cuando se observan a escala microscópica.
CLASES DE ROZAMIENTO POR DESLIZAMIENTO
A) Rozamiento Estático
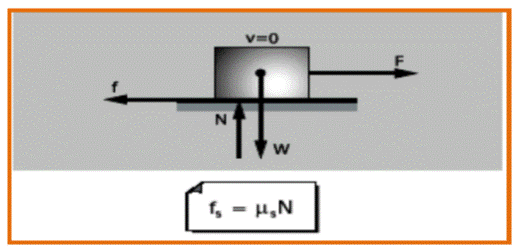
Es la que se presenta entre superficies que se encuentran en reposo. El valor de la fuerza de rozamiento estático varía desde cero hasta un valor máximo, el cual lo adquiere cuando el cuerpo en contacto está a punto de moverse, pero sin conseguirlo (movimiento inminente).
Este valor máximo de la fuerza de rozamiento estático equivale a la fuerza mínima para iniciar el movimiento, el cual puede calcularse mediante la siguiente fórmula.
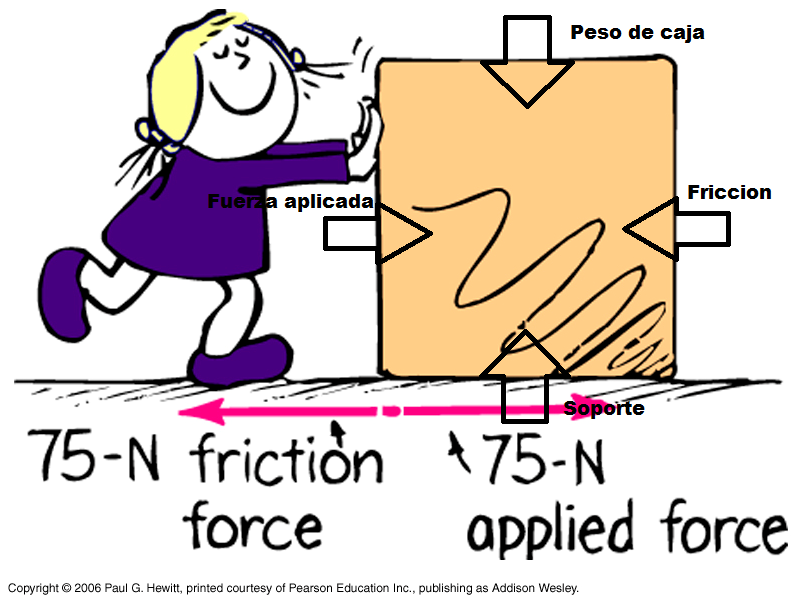
fs=μs • N
Siendo:
fs=Fuerza de roce estático máximo
μs= Coeficiente de roce estático
N= Fuerza Normal
B) Rozamiento Cinético
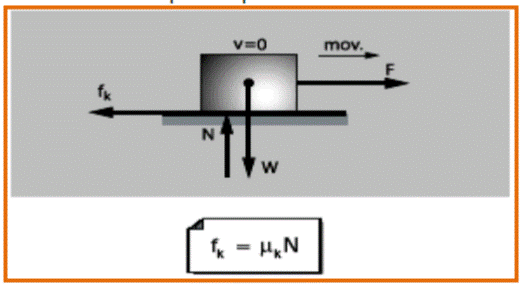
Es aquella que se presenta cuando hay movimiento de un cuerpo respecto al otro.
Cuando el cuerpo pasa del movimiento inminente al movimiento propiamente dicho, el valor de la fuerza de rozamiento disminuye y permanece casi constante, si es que la velocidad no es muy grande. (Entre 0,01 m/s y 20 m/s).
Se puede calcular mediante:
fc=μc • N
Siendo:
fc=Fuerza de roce cinético
μc= Coeficiente de roce cinético
N= Fuerza Normal
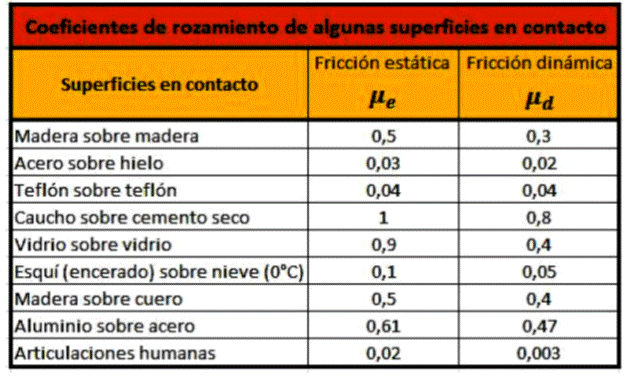
El coeficiente de rozamiento depende del tipo de materiales de las superficies en contacto.
El coeficiente de rozamiento cinético (μK) siempre es menor que el estático (μe)
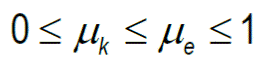
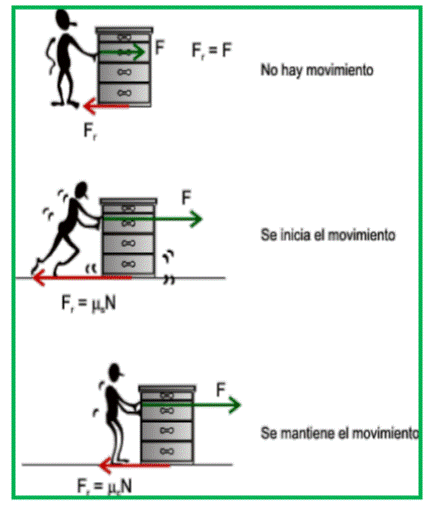
Cuando un cuerpo sobre una superficie se empuja o se jala éste puede permanecer inmóvil, esto sucede porque la fuerza aplicada no ha sido suficiente para vencer la fuerza de fricción. Cuando logramos que el cuerpo deslice sobre la superficie es necesario aplicar una fuerza para que éste continúe en movimiento.
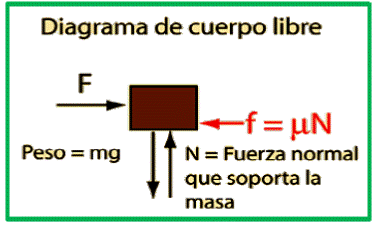
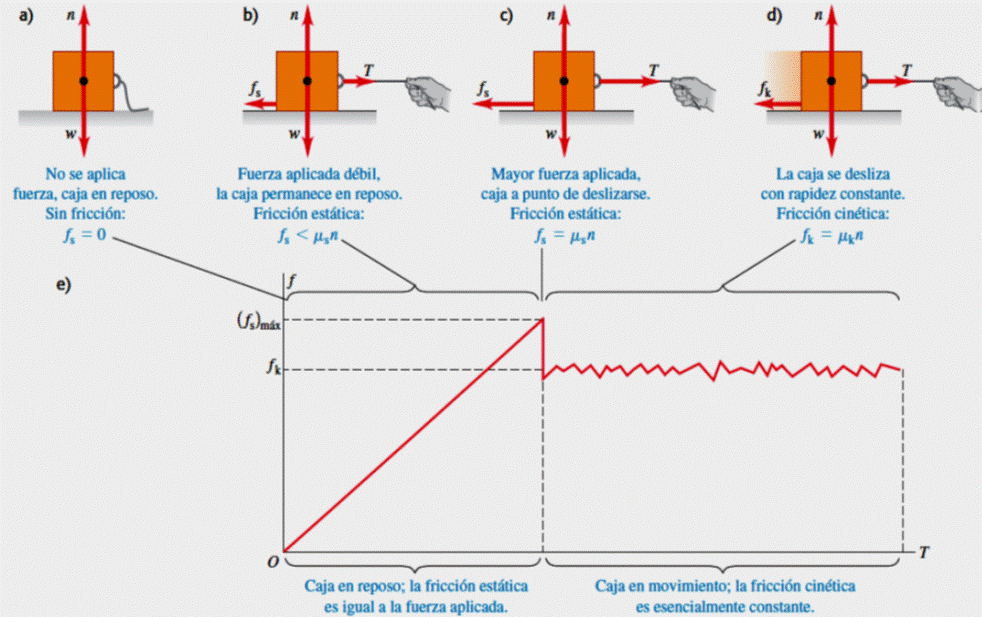
Comportamiento de un cuerpo que descansa sobre un plano horizontal
Supongamos que jalamos un bloque con un dinamómetro, como se muestra en la figura.
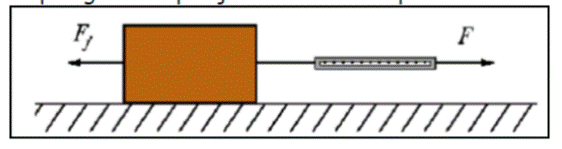
Dibujemos una gráfica de la fuerza F aplicada sobre el bloque versus el tiempo t
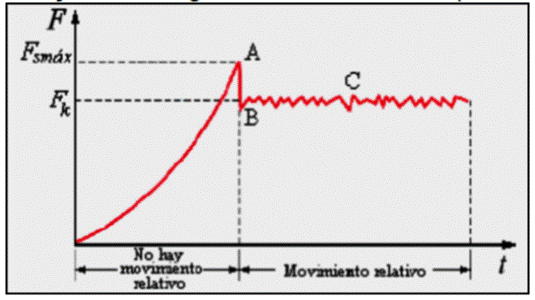
1. Desde el origen hasta el punto A la fuerza F aplicada sobre el bloque no es suficientemente grande como para moverlo. Estamos en una situación de equilibrio estático.
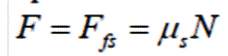
En el punto A, la fuerza de rozamiento fs alcanza su máximo valor N μs máximo
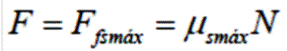
2. Si la fuerza F aplicada se incrementa un poquito más, el bloque comienza a moverse. La fuerza de rozamiento disminuye rápidamente a un valor menor e igual a la fuerza de rozamiento dinámico

Si la fuerza F no cambia, punto B, y permanece igual a fs máx , el bloque comienza moviéndose con una aceleración
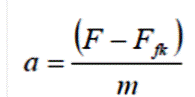
Si incrementamos la fuerza F, punto C, la fuerza neta sobre el bloque se incrementa y también se incrementa la aceleración.
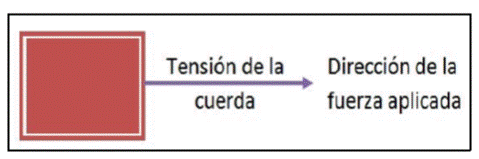
4.- Tensión (T):

La tensión es una fuerza que convencionalmente aparece siempre asociada a situaciones en las que se tira de un cuerpo con ayuda de un cable o de una cuerda. Cuando una cuerda está tensa, ejerce
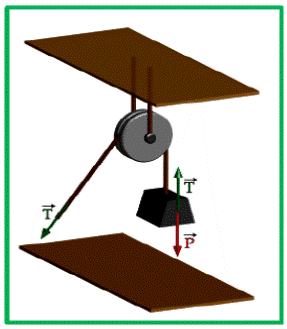
una fuerza sobre el cuerpo llamada tensión. Estos cables o cuerdas cumplen con dos condiciones esenciales, son de masa despreciables y se asumen como prácticamente inextensibles.
La tensión T es la fuerza que puede existir debido a la interacción en un resorte, cuerda o cable cuando está atado a un cuerpo y se jala o tensa. Esta fuerza ocurre hacia fuera del objeto y es paralela al resorte, cuerda o cable en el punto de la unión.
MOVIMIENTO DE UN CUERPO SOBRE SUPERFICIES HORIZONTALES
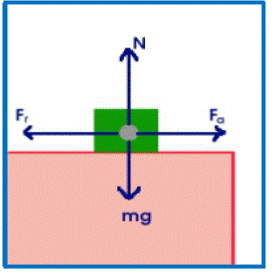
El movimiento de un cuerpo sobre un plano horizontal al que se le aplica una fuerza. La fuerza que actúa sobre el cuerpo perpendicularmente al plano de deslizamiento es su peso:
Peso = m · g
y según la figura de la derecha se cumple
N=Peso=m·g
Por tanto, la fuerza de rozamiento (la cinética, siempre) valdrá:
Fr=μ·N=μ·m·g
La fuerza efectiva que dé origen a la aceleración del objeto será:
Fefectiva=Faplicada- Fr=Fa- μ·m·g
FUERZA ELÁSTICA, LEY DE HOOKE

Si un cuerpo después de ser deformado por una fuerza, vuelve a su forma o tamaño original cuando deja de actuar la fuerza deformadora se dice que es un cuerpo elástico.
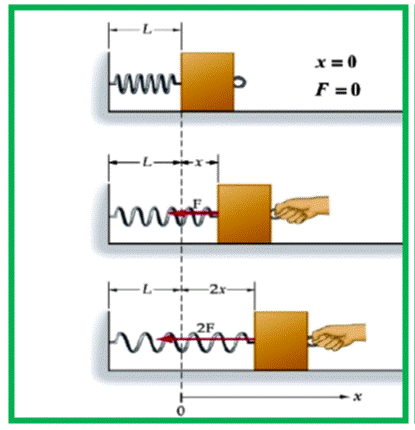
Las fuerzas elásticas reaccionan contra la fuerza deformadora para mantener estable la estructura molecular del sólido.
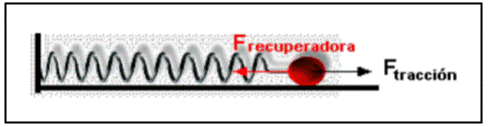
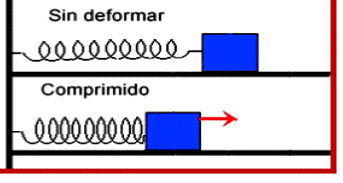
La ley de fuerza para el resorte es la Ley de Hooke. Conforme el resorte está estirado (o comprimido) cada vez más, la fuerza de restauración del resorte se hace más grande y es necesario aplicar una fuerza mayor.
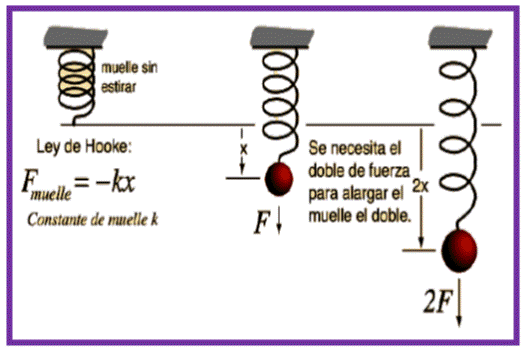
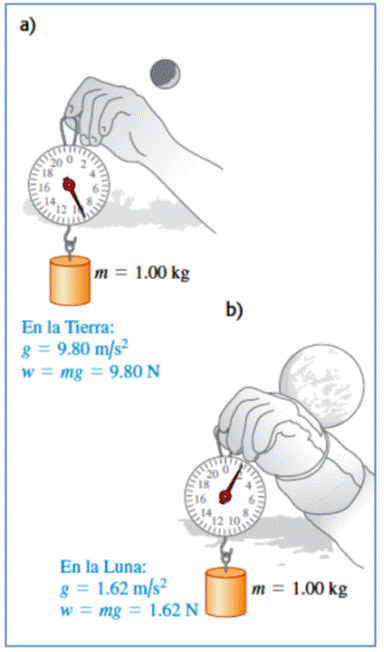
En las figuras, ya sea el eje horizontal o vertical, se aprecia que cuando la fuerza en el resorte es F = 0, el resorte no tiene elongación, o sea X = 0; si se aplica una fuerza de módulo F, el resorte adquiere una elongación X; ahora si se duplica la fuerza (2F), se elongará el doble (2X). Según lo anterior se encuentra que la fuerza aplicada F es directamente proporcional al desplazamiento X o al cambio de longitud del resorte.
Hooke estableció la ley fundamental que relaciona la fuerza aplicada y la deformación producida. Para una deformación unidimensional, la Ley de Hooke se puede expresar matemáticamente así:
F= - K X
Donde:
• K es la constante de proporcionalidad o de elasticidad, (Newton/ metro)
• X es la deformación, esto es, lo que se ha comprimido o estirado a partir del estado que no tiene deformación. Se conoce también como el alargamiento de su posición de equilibrio, (metro)
• F es la fuerza, (Newton)
• El signo ( - ) en la ecuación se debe a la fuerza restauradora que tiene sentido contrario al desplazamiento. La fuerza se opone o se resiste a la deformación.
Como se puede ver la fuerza varía con la longitud X, de compresión o elongación. Esto se expresa diciendo que la fuerza es una función de la posición. La “K” en esta ecuación es una constante de proporcionalidad y comúnmente se llama la constante de elasticidad del resorte o de la fuerza restauradora. Mientras mayor sea el valor de K, más rígido o fuerte será el resorte.
Fue Robert Hooke (1635-1703), físico-matemático, químico y astrónomo inglés, quien primero demostró el comportamiento sencillo relativo a la elasticidad de un cuerpo. Hooke estudió los efectos producidos por las fuerzas de tensión, observó que había un aumento de la longitud del cuerpo que era proporcional a la fuerza aplicada.
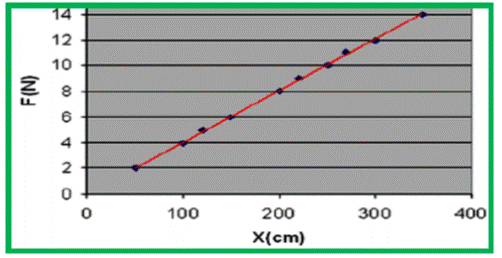
Como ya se dijo anteriormente, la deformación que experimenta un cuerpo es directamente proporcional al esfuerzo producido. Dicha relación entre ambas magnitudes se la conoce como Ley de Hooke.
En este gráfico se muestra una síntesis de lo que trata dicha ley:
EFECTO DE LA FUERZA DE GRAVEDAD (PESO) EN UN RESORTE
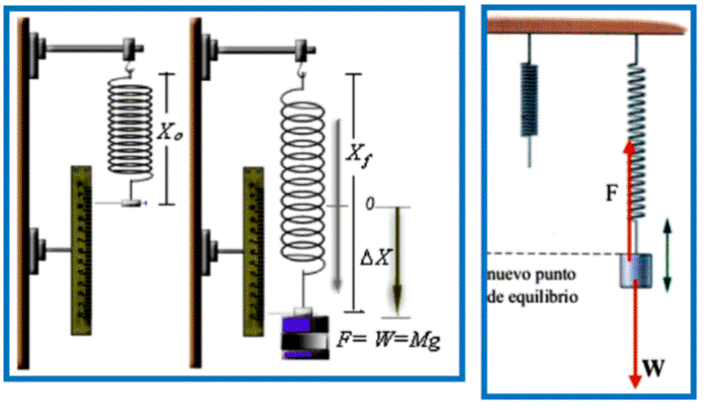
Si a un resorte que está en la posición de equilibrio, en X0 = 0, se le suspende una masa m, hará que dicho resorte experimente un estiramiento, en este caso de magnitud ΔX = X. Esta variación de longitud se debe a la fuerza gravitacional, fuerza peso (F=W= Peso= Mg), de sentido vertical hacia abajo. A su vez está actuando en sentido inverso al peso la fuerza elástica, de restitución del resorte.
- Según la Ley de Hooke:
FElast.= K ⋅ X (1)
- En el equilibrio, se cumple:
FElast. = Peso (2)
- Además:
Peso = m ⋅ g (3)
Donde:
m= Masa del cuerpo colgante
g = Aceleración de gravedad
gTierra= 9,8 m/s2 ≈ 10 m/s2
Reemplazando, (2) en (1):
Peso = K ⋅ X
m g = K ⋅X
Finalmente, para obtener el valor de la constante de elasticidad, K:
K= m g / X
Ejemplo: Supongamos que en un resorte se colgaron 7 masas distintas, obteniéndose los siguientes datos y gráfico:
Al calcular la pendiente de la recta, se obtiene la constante de elasticidad K del resorte, es decir:
fifiP - P Pendiente = K = - XX, 35 - 5 30NK = 50 0,70 - 0,100,60m==
El dinamómetro es un instrumento utilizado para medir fuerzas o para pesar objetos. El dinamómetro tradicional, inventado por Isaac Newton, basa su funcionamiento en el estiramiento de un resorte que sigue la ley de elasticidad de Hooke en el rango de medición. Al igual que una báscula con resorte elástico, es una balanza de resorte,
pero no debe confundirse con una balanza de platillos (instrumento utilizado para comparar masas). Estos instrumentos constan de un resorte, generalmente contenido en un cilindro que a su vez puede estar introducido en otro cilindro. El dispositivo tiene dos ganchos o anillas, uno en cada extremo. Los dinamómetros llevan marcada una escala en el cilindro hueco que rodea al resorte. Al colgar pesos o ejercer una fuerza sobre el gancho exterior, el cursor de ese extremo se mueve sobre la escala exterior, indicando el valor de la fuerza. El dinamómetro funciona gracias a un resorte o espiral que tiene en el interior, el cual puede alargarse cuando se aplica una fuerza sobre él. Una aguja o indicador suele mostrar, paralelamente, la fuerza.
Otras aplicaciones indirectas de la ley de Hooke pueden ser observadas en todos los mecanismos que poseen resortes; como relojes analógicos, ellos poseen generalmente resortes de torsión, los que tienen forma de espiral, pero cumplen de igual forma con la ley de Hooke. En la suspensión de los automóviles se utilizan resortes de compresión los que tienen una constante elástica muy alta haciendo también que el valor de la fuerza restauradora sea grande ya que esta se opone al peso del automóvil.
-
-
-