Diagrama de temas
-
-
Foro
-
Foro
-
-
-
-

En la vida cotidiana

aparecen muchos fenómenos asociados a las ondas, denominados ondulatorios.
En física, una onda es una propagación de una perturbación de alguna propiedad de un medio, por ejemplo, densidad, presión, campo eléctrico o campo magnético, que se propaga a través del espacio transportando energía. El medio perturbado puede ser de naturaleza diversa como aire, agua, un trozo de metal, el espacio o el vacío.
Los fenómenos ondulatorios tienen unas propiedades específicas, que nos permiten hablar, oír o ver, y sirven para transmitir energía sin que haya un transporte de materia.
Mediante el sonido nos comunicamos con los demás, experimentamos el placer al escuchar música, mientras que la luz activa el sentido de la vista, proporcionándonos la mayor parte de la información del mundo que nos rodea.
La luz y la radiación electromagnética muestran cómo es el Universo y mediante radiaciones electromagnéticas nos comunicamos, casi instantáneamente, a largas distancias.
Las propiedades de los fenómenos ondulatorios tienen múltiples aplicaciones tecnológicas como el diagnóstico médico por medio de ecografías, la determinación de distancias mediante el sonar de los barcos o el desarrollo de nuevas fuentes de luz como el láser, que ha revolucionado el mundo de las comunicaciones y de la transmisión de información mediante ondas electromagnéticas.
Más de una vez hemos visto las ondas producidas en la superficie del agua de un estanque al dejar caer en ella una piedra, o las formadas en una cuerda cuando la sacudimos. ¿Qué tienen en común todas estas ondas? ¿Qué las caracteriza?

ONDAS TRANSPORTADORAS DE ENERGÍA Y NO MATERIA
Las ondas producidas en el agua solamente desplazan arriba y abajo cualquier objeto que flote en ella, como un trozo de corcho, pero no lo desplazan en la dirección en que avanzan las ondas. Cuando el agua queda en reposo, el objeto se encuentra en su posición inicial. Este hecho se interpreta admitiendo que la onda, al propagarse por la superficie del agua, no realiza un transporte neto de las partículas
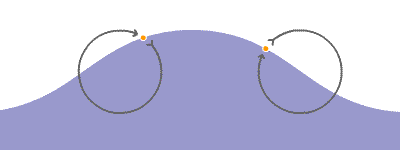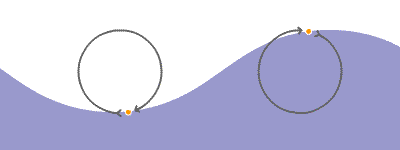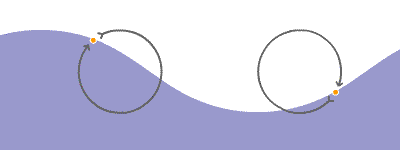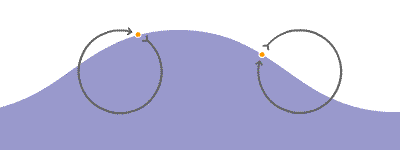
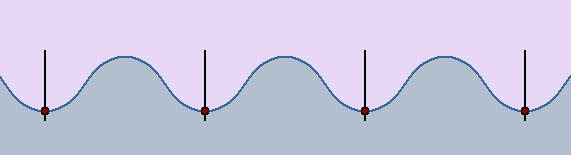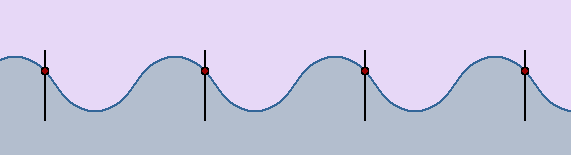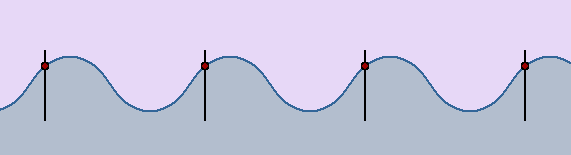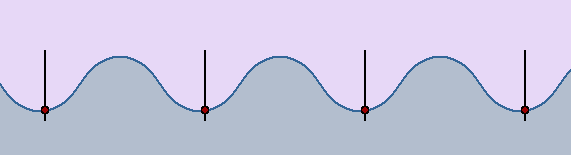
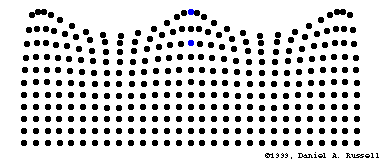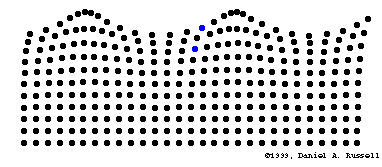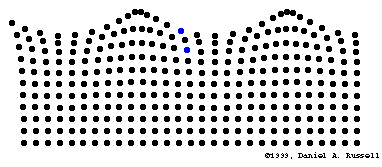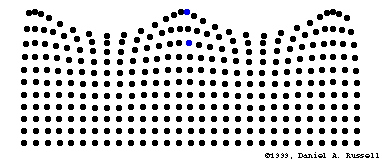

Un movimiento ondulatorio es una forma de transmisión de energía, sin transporte neto de materia, mediante la propagación de alguna forma de perturbación. Esta perturbación se denomina onda.
ENERGY%20WAVES%20CLIP%20%282%29.mp3
Energy Waves
Kenny Hood
Energy can be carried
from one place to another by waves,
water waves and sound waves.
Energy can also be moved
by electric currents
and moving objects.Energy moves in many ways
through moving objects,
electricity, and even waves.
Many things we use
and everything we say
travels in light, sound, seismic,
or ocean waves!Energy and a playground ball...
if it’s held in you hand,
no motion transfer at all.
Once you wind up and toss it
on over to your friend,
the energy travels from you,
to the ball, to your friend
at the end.CLASIFICACIÓN DE LAS ONDAS
CLASIFICACIÓN EN FUNCIÓN DE SU PROPAGACIÓN O FRENTE DE ONDA
- Ondas unidimensionales: las ondas unidimensionales son aquellas que se propagan a lo largo de una sola dirección del espacio, como las ondas en los resortes o en las cuerdas. Si la onda se propaga en una dirección única, sus frentes de onda son planos y paralelos.

- Ondas bidimensionales o superficiales: son ondas que se propagan en dos direcciones. Pueden propagarse, en cualquiera de las direcciones de una superficie, por ello, se denominan también ondas superficiales. Un ejemplo son las ondas que se producen en una superficie líquida en reposo cuando, por ejemplo, se deja caer una piedra en ella.

- Ondas tridimensionales o esféricas: son ondas que se propagan en tres direcciones. Las ondas tridimensionales se conocen también como ondas esféricas, porque sus frentes de ondas son esferas concéntricas que salen de la fuente de perturbación expandiéndose en todas direcciones. El sonido es una onda tridimensional. Son ondas tridimensionales las ondas sonoras (mecánicas) y las ondas electromagnéticas.

CLASIFICACIÓN EN FUNCIÓN DE SU PERIODICIDAD
- Ondas periódicas: la perturbación local que las origina se produce en ciclos repetitivos por ejemplo una onda senoidal.
- Ondas no periódicas: la perturbación que las origina se da aisladamente o, en el caso de que se repita, las perturbaciones sucesivas tienen características diferentes. Las ondas aisladas se denominan también pulsos.
CLASIFICACIÓN EN FUNCIÓN DE LA DIRECCIÓN DE LA PERTURBACIÓN
- Ondas transversales: Si en el extremo libre de una cuerda tensa horizontal damos una sacudida vertical repentina, se forma una cresta o protuberancia llamada pulso de onda o simplemente pulso. Este es una perturbación instantánea que se transmite mediante una onda viajera y recorre la cuerda desplazando los distintos puntos de ésta hacia arriba y hacia abajo para volver a la posición inicial apenas pasa la onda.


Si mantenemos un movimiento vibratorio haciendo oscilar la cuerda arriba y abajo repetidas veces, y de forma periódica, se produce una perturbación continua, denominada tren de ondas, que se propaga por la cuerda. Las partículas de ésta se desplazan verticalmente en torno a su posición de equilibrio.
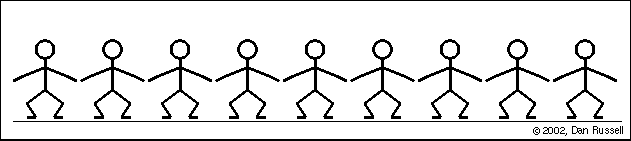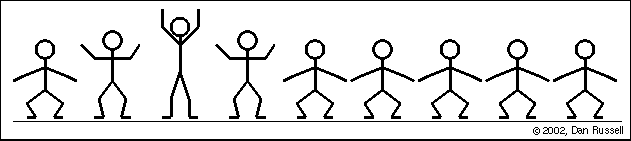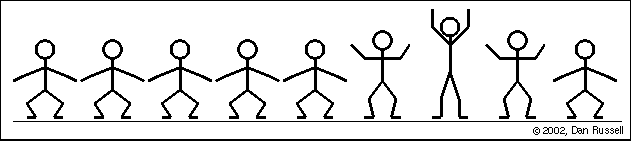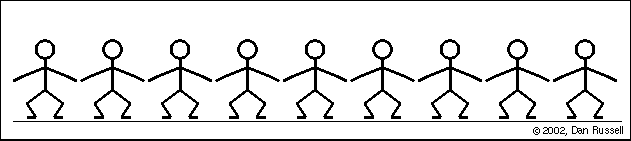


Una onda es transversal si su dirección de propagación es perpendicular (90°) a la dirección de la oscilación que provoca en las partículas del medio perturbado.
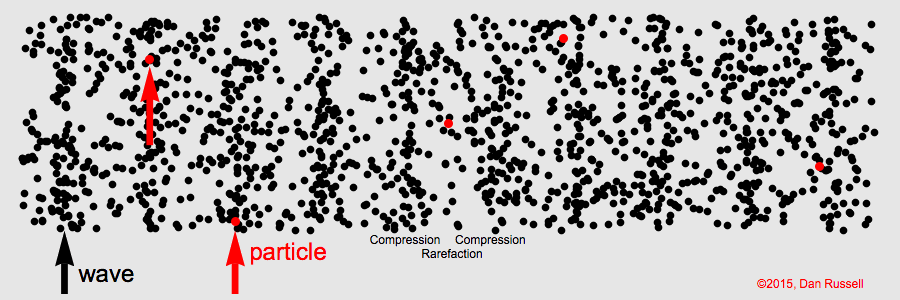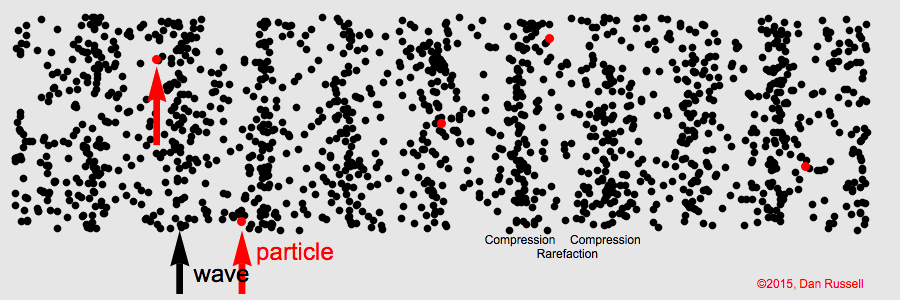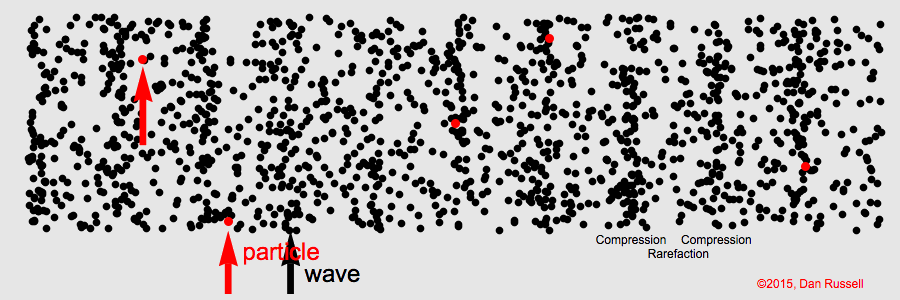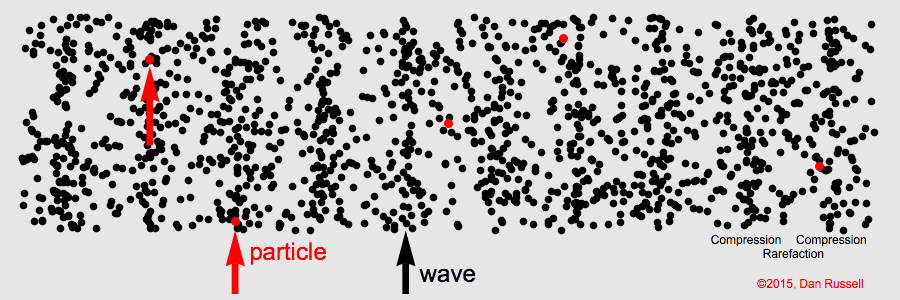
- Ondas longitudinales: A un resorte, fijo por un extremo y en posición horizontal, le aplicamos un movimiento repentino de compresión y expansión a derecha e izquierda. El pulso de onda producido da lugar a que la región comprimida de las espiras se propague a lo largo del resorte. Hemos provocado la formación de una onda viajera longitudinal.



La repetición de estos impulsos provoca la aparición de un tren de ondas similares; cada región comprimida va seguida de una zona distendida.
Las ondas sonoras son un ejemplo típico de esta clase de ondas (longitudinales).



CLASIFICACIÓN DE LAS ONDAS SEGÚN NECESITEN O NO UN MEDIO MATERIAL PARA PROPAGARSE.
- Ondas mecánicas: Propagación de una perturbación de tipo mecánico a través de algún medio material elástico por el que se transmite la energía mecánica de la onda. El medio material puede ser el aire, el agua, una cuerda... y es indispensable para la existencia de la onda.
Ejemplos de ellas son las ondas sonoras, las producidas en una cuerda de una guitarra entre muchas otras y al comunicarse con otra persona mediante un cordel.

mario-bross-remix-guitarra-%20%281%29.mp3
- Ondas electromagnéticas: Son aquellas ondas que no necesitan un medio material para propagarse. Incluyen, entre otras, la luz visible y las ondas de radio, televisión y telefonía.


Las ondas electromagnéticas se dispersan en el espacio al igual que lo hacen los rizos que se forman en un lago cuando se arroja una piedra en sus aguas.
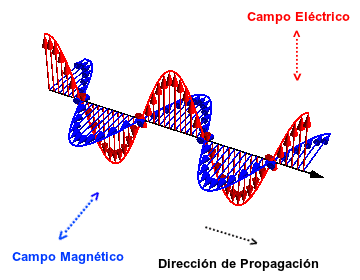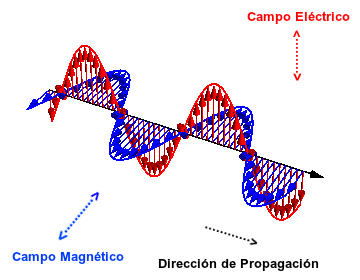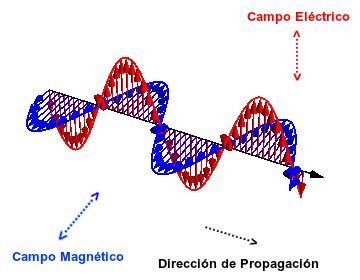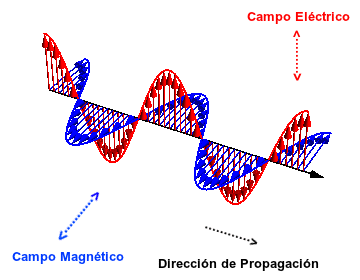




Todas se propagan en el vacío a una velocidad constante, muy alta (300.000 km/s) pero no infinita. Gracias a ello podemos observar la luz emitida por una estrella lejana hace tanto tiempo que quizás esa estrella haya desaparecido ya. O enterarnos de un suceso que ocurre a miles de kilómetros prácticamente en el instante de producirse.
CARACTERÍSTICAS DE LAS ONDAS ARMÓNICAS TRANSVERSALES
Para estudiar las características de las ondas, se va a usar ondas transversales y armónicas (simétricas). Dichas características son aplicables a las ondas longitudinales. Se tomarán como ejemplo la producción en un tren de ondas armónicas transversales.
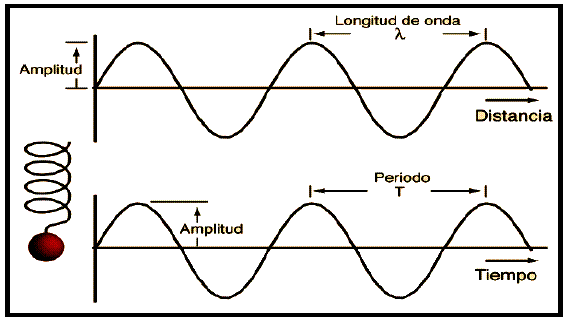
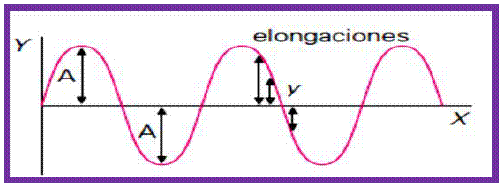
- Elongación: Es la distancia entre cada punto en su estado de vibración y la posición central de equilibrio, siendo la amplitud (A) la máxima separación de la partícula de la posición central o de equilibrio.
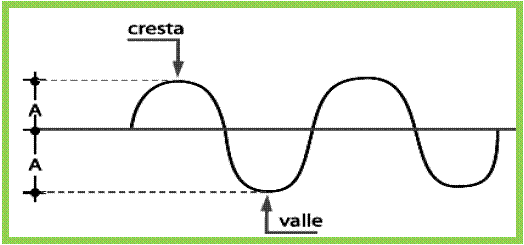
- Amplitud de la onda, A: Corresponde a la elongación máxima, al máximo valor que alcanza una perturbación respecto a su posición de equilibrio. Es la distancia vertical (en este caso) entre el punto más alto (cresta) y su posición de equilibrio, o entre el más bajo (valle) y su posición de equilibrio. Su unidad en el S.I. (sistema internacional de unidades) es el metro, m.
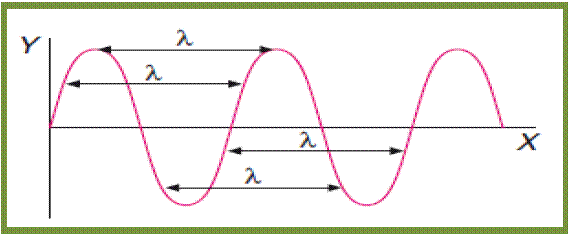
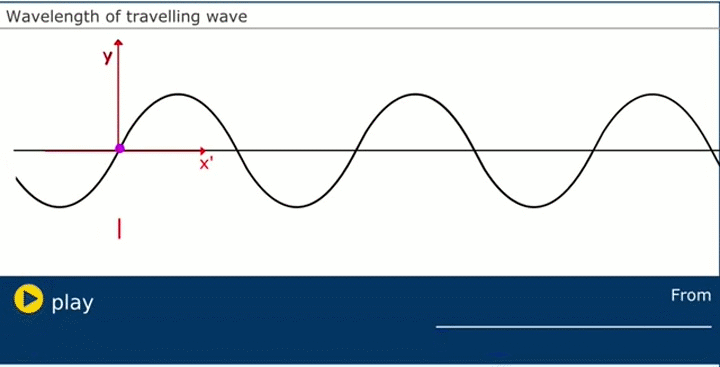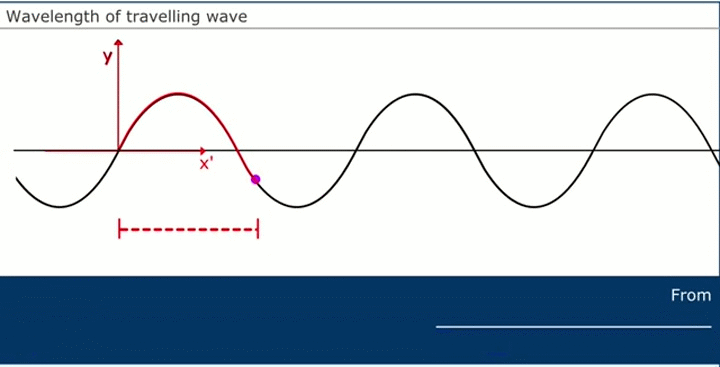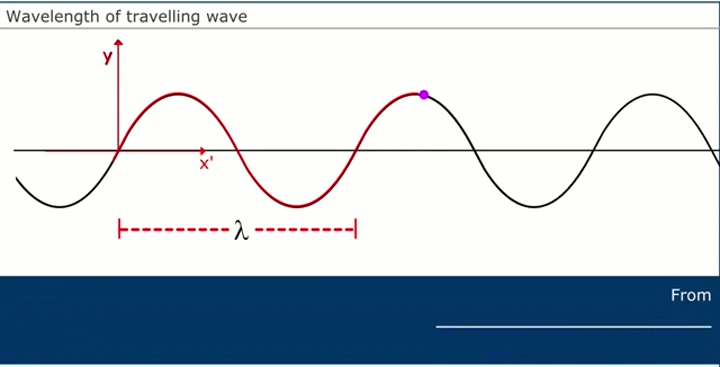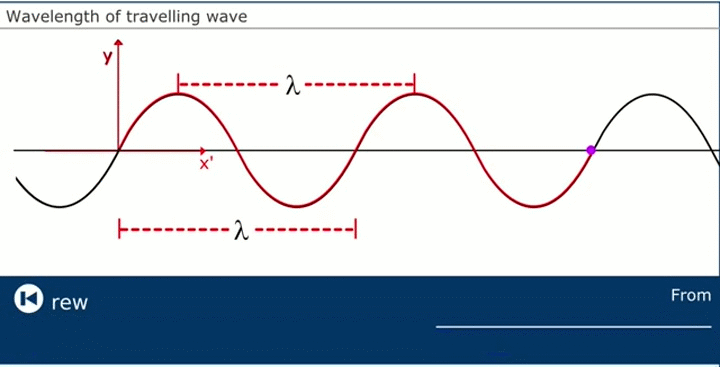
- Longitud de onda, λ (lambda): Es la distancia mínima entre dos puntos consecutivos equivalentes que se hallan en el mismo estado de vibración, también se puede definir como la distancia horizontal (en este caso) de una oscilación completa. Su unidad en el S.I. es el metro, m.

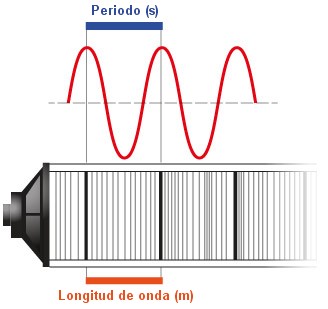
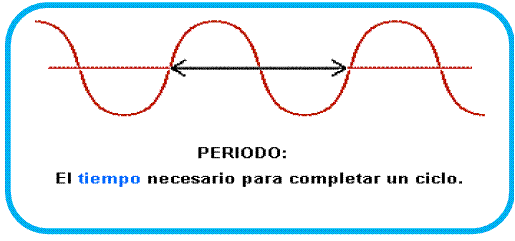
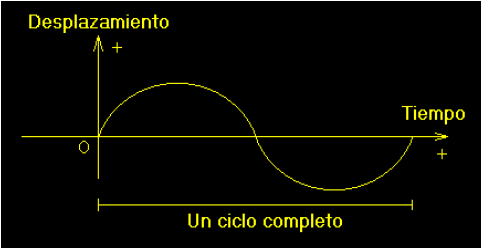
- Período, T: Es el tiempo que tarda la onda en recorrer una distancia igual a su longitud de onda, o bien el tiempo que emplea un punto cualquiera afectado por la perturbación en efectuar una oscilación completa. Su unidad de medida en el S.I. es el segundo, s.
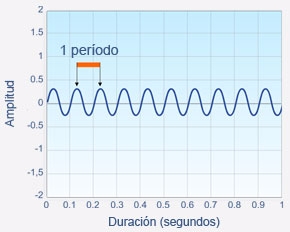
- Frecuencia, f: Es el número de ondas que pasan por un punto del medio por unidad de tiempo. También puede definirse como el número de oscilaciones que efectúa un punto del medio por unidad de tiempo, es decir: N° de oscilaciones por cada segundo

Su unidad en el S.I. es el hertz (hercio), Hz, igual a 1/s ó s-1.
La unidad hercio, Hertz (HZ) es en honor al físico alemán Heinrich Hertz (1875-1894), que demostró la existencia de ondas electromagnéticas y puso las bases de la telegrafía sin hilos.
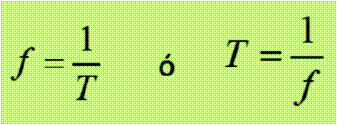
Al relacionar frecuencia f con el periodo T se puede apreciar que ambas son inversamente proporcionales, entonces se cumple:
-
 Rapidez de propagación de una onda,
v: Es aquella rapidez con que
se propaga una perturbación en el medio. Esta rapidez es una
característica del medio en que la onda se propaga. De la
cinemática se define la rapidez como el cuociente entre la
distancia y el tiempo empleado, es decir:
Rapidez de propagación de una onda,
v: Es aquella rapidez con que
se propaga una perturbación en el medio. Esta rapidez es una
característica del medio en que la onda se propaga. De la
cinemática se define la rapidez como el cuociente entre la
distancia y el tiempo empleado, es decir:
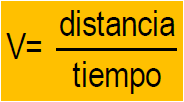
como la longitud de onda λ corresponde a la distancia recorrida por una perturbación en un tiempo equivalente a un periodo “T”, al reemplazar se obtiene:
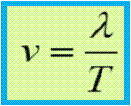
utilizando ,
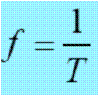
también se deduce:
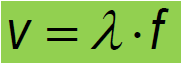
-
-

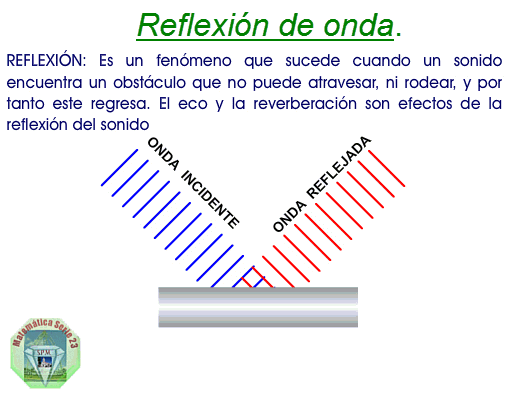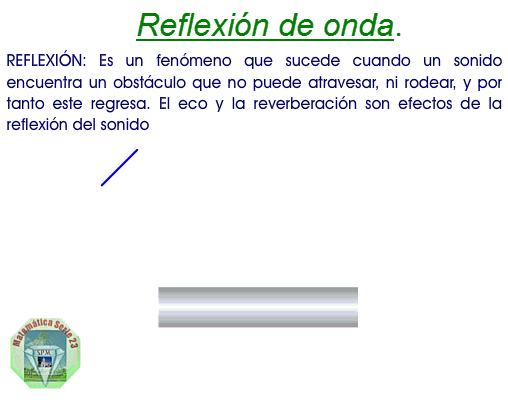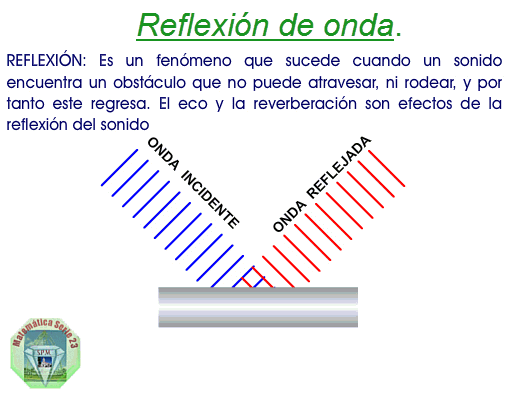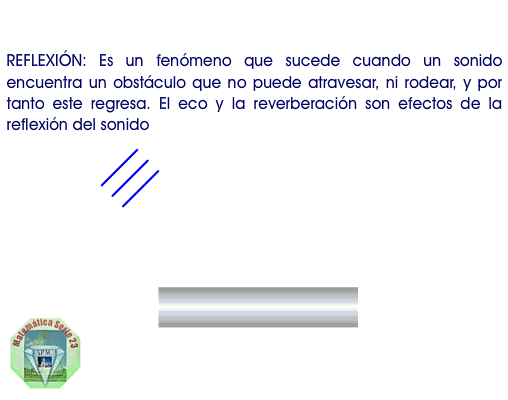
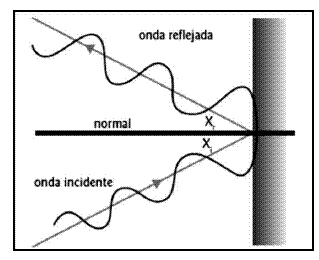 Reflexión: Si un medio material no permite que
una onda siga propagándose, ésta
“rebota”, es decir, se refleja y se cumple que “la onda
incidente, la onda reflejada y la
normal están en un mismo plano”
(primera ley de la reflexión) y “el ángulo
de incidencia es congruente con el
ángulo de reflexión” (segunda ley
de la reflexión). La reflexión se
produce cuando una onda encuentra en su
camino un medio de propagación más
denso.
Reflexión: Si un medio material no permite que
una onda siga propagándose, ésta
“rebota”, es decir, se refleja y se cumple que “la onda
incidente, la onda reflejada y la
normal están en un mismo plano”
(primera ley de la reflexión) y “el ángulo
de incidencia es congruente con el
ángulo de reflexión” (segunda ley
de la reflexión). La reflexión se
produce cuando una onda encuentra en su
camino un medio de propagación más
denso.
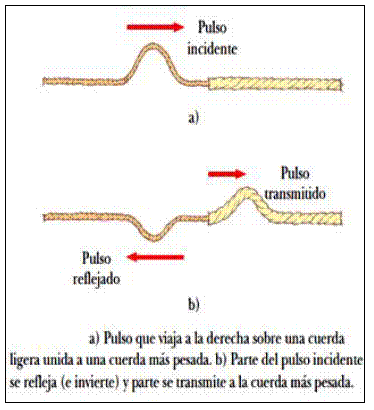
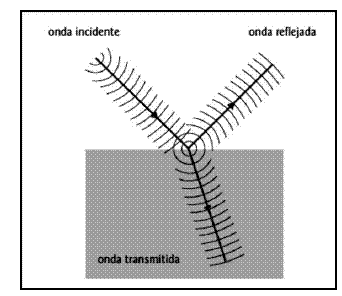 Transmisión: Cuando una
onda pasa de un medio a otro, parte de esta se devuelve
(reflexión) y otra parte pasa al nuevo medio (transmisión). En
este proceso no hay pérdida de energía, ya que la suma de la
energía de la onda reflejada y la transmitida es equivalente a
la energía de la onda incidente, si sumáramos las amplitudes de
las ondas reflejada y transmitida, esta debe ser equivalente a
la amplitud de la onda incidente.
Transmisión: Cuando una
onda pasa de un medio a otro, parte de esta se devuelve
(reflexión) y otra parte pasa al nuevo medio (transmisión). En
este proceso no hay pérdida de energía, ya que la suma de la
energía de la onda reflejada y la transmitida es equivalente a
la energía de la onda incidente, si sumáramos las amplitudes de
las ondas reflejada y transmitida, esta debe ser equivalente a
la amplitud de la onda incidente.
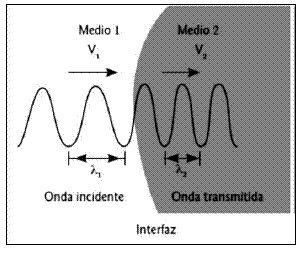 En la transmisión la onda
mantiene su frecuencia, variando su longitud de onda, lo que
hace que se modifique su rapidez de propagación (v = λ ⋅
f)
En la transmisión la onda
mantiene su frecuencia, variando su longitud de onda, lo que
hace que se modifique su rapidez de propagación (v = λ ⋅
f)
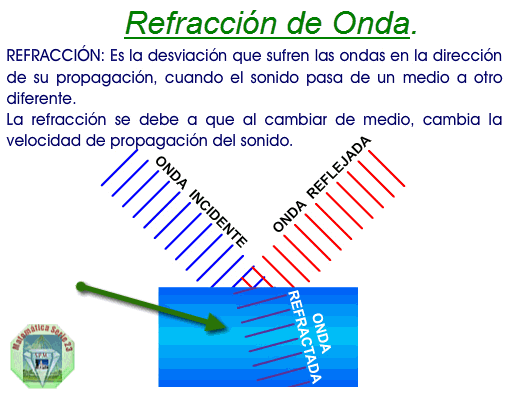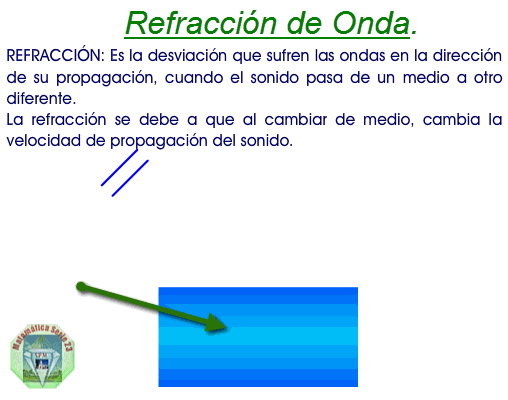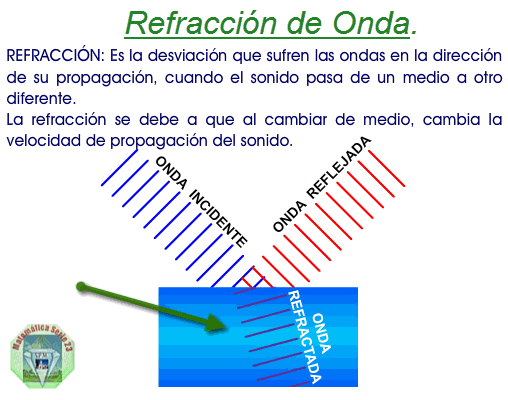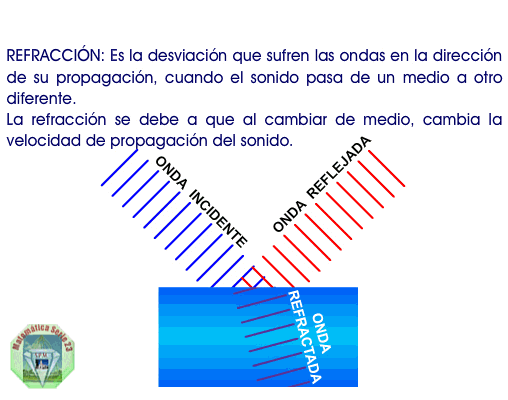
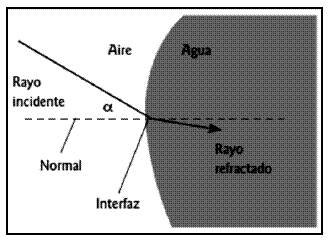 Refracción: Cuando una
onda pasa de un medio a otro, generalmente cambia su dirección
de propagación (esto no ocurre sólo cuando incide
perpendicularmente a la superficie de contacto de los dos
medios).
Refracción: Cuando una
onda pasa de un medio a otro, generalmente cambia su dirección
de propagación (esto no ocurre sólo cuando incide
perpendicularmente a la superficie de contacto de los dos
medios).
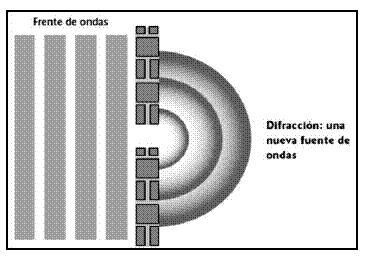
Difracción: Si una onda es interrumpida parcialmente por un obstáculo en su dirección de propagación, la onda puede rodearlo y seguir propagándose. Cuando hay dos obstáculos que delimitan un pequeño espacio, las ondas también pueden pasar.
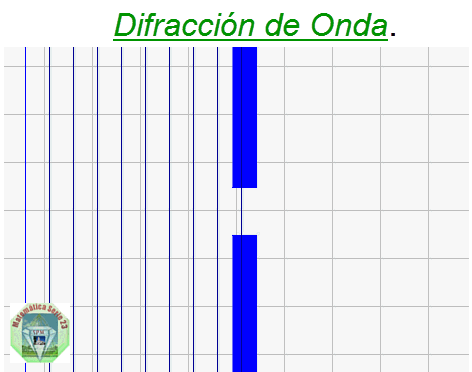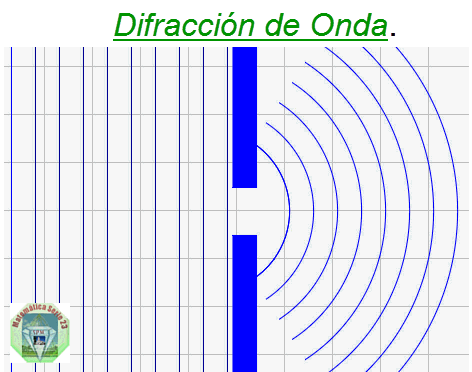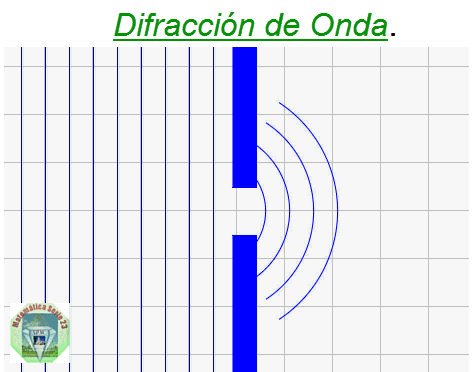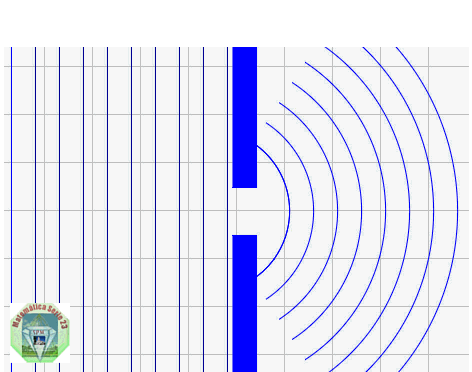
Superposición e Interferencia: Muchos fenómenos ondulatorios interesantes en la naturaleza no pueden describirse mediante una sola onda en movimiento. En lugar de ello es necesario analizar formas de onda complejas en función de una combinación de diferentes ondas viajeras. Para analizar dichas combinaciones de onda se utiliza el principio de superposición de ondas.
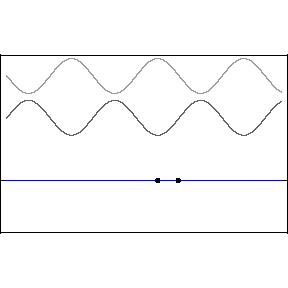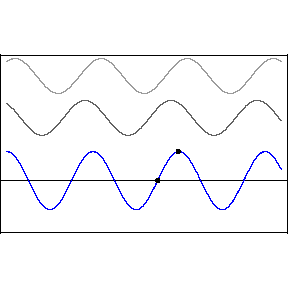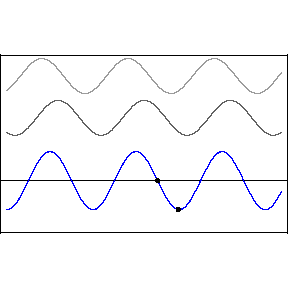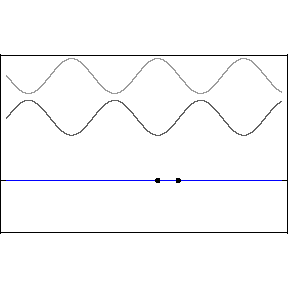
El principio de superposición establece que si dos o más ondas viajeras se mueven a través de un medio, la función de onda resultante en cualquier punto es la suma algebraica de las funciones de onda individuales.
Dos ondas viajeras pueden pasar una a través de otra sin alterarse. Decimos que cuando dos o más ondas ocupan la misma posición en un cierto momento, necesariamente se interfieren. A este fenómeno de interacción entre ondas se denomina interferencia.
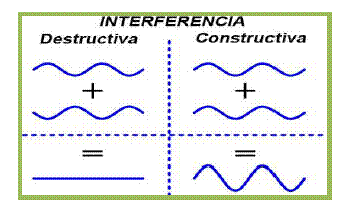
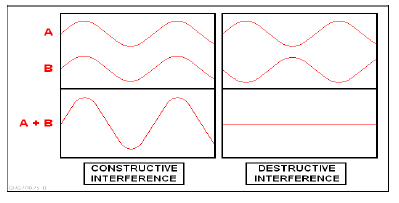
- Interferencia constructiva
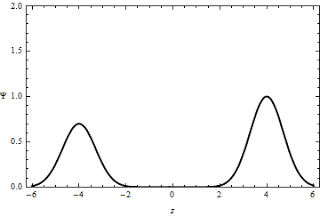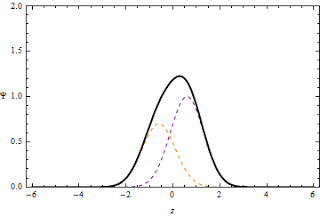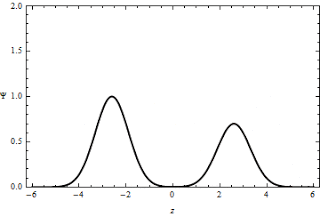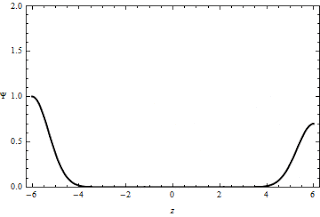
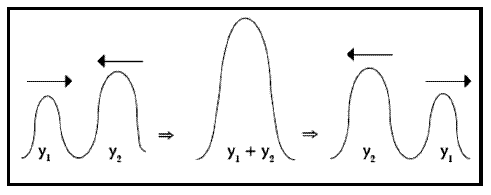 Supongamos dos pulsos de
amplitud y1 e y2 viajando en una cuerda
tensa uno al encuentro del otro, ambos en sentido “y” positivo.
Al momento de interferirse sus amplitudes respectivas se
adicionan, de tal forma que la onda instantánea resultante en
dicho punto presentará una elongación máxima (y1 +
y2) mayor a las amplitudes individuales de cada uno
de los pulsos originales. En este caso hablaremos de
interferencia constructiva.
Supongamos dos pulsos de
amplitud y1 e y2 viajando en una cuerda
tensa uno al encuentro del otro, ambos en sentido “y” positivo.
Al momento de interferirse sus amplitudes respectivas se
adicionan, de tal forma que la onda instantánea resultante en
dicho punto presentará una elongación máxima (y1 +
y2) mayor a las amplitudes individuales de cada uno
de los pulsos originales. En este caso hablaremos de
interferencia constructiva.
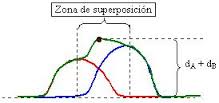
- Interferencia destructiva
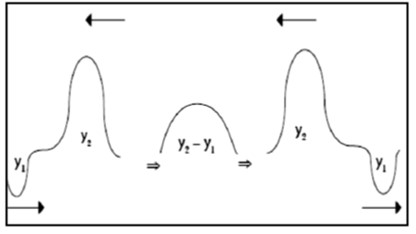 Consideremos ahora, dos pulsos de
amplitud y1 e y2 que viajan también uno
al encuentro del otro, pero en sentidos opuestos de “y”, como
indica la siguiente figura. En este caso, cuando los pulsos se
superpongan, la onda instantánea resultante en dicho punto
presentará una amplitud (y1-y2). En este
caso hablaremos de interferencia destructiva. Nuevamente ambos
pulsos se atraviesan mutuamente para seguir su propagación
individual.
Consideremos ahora, dos pulsos de
amplitud y1 e y2 que viajan también uno
al encuentro del otro, pero en sentidos opuestos de “y”, como
indica la siguiente figura. En este caso, cuando los pulsos se
superpongan, la onda instantánea resultante en dicho punto
presentará una amplitud (y1-y2). En este
caso hablaremos de interferencia destructiva. Nuevamente ambos
pulsos se atraviesan mutuamente para seguir su propagación
individual.
Interferencia constructiva en una cuerda:
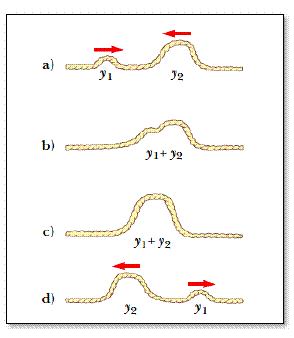
a) y d) dos pulsos que viajan en direcciones opuestas en una cuerda estirada pasan una a través de la otra. Cuando los pulsos se traslapan, como se muestra en b) y c), el desplazamiento neto de la cuerda es igual a la suma de los desplazamientos producidos por cada pulso. Ya que cada pulso produce desplazamientos positivos de la cuerda, a su sobreposición se le refiere como interferencia constructiva.
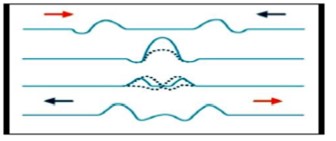
Interferencia destructiva en una cuerda:
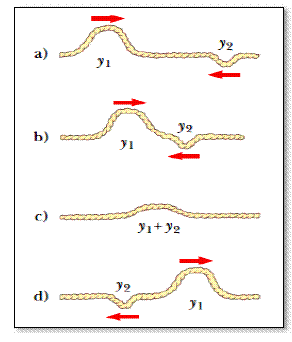 a) y d) dos pulsos que
viajan en direcciones opuestas y tienen desplazamientos
invertidos uno en relación con el otro. Cuando los dos se
traslapan en c), sus desplazamientos se cancelan parcialmente
uno a otro.
a) y d) dos pulsos que
viajan en direcciones opuestas y tienen desplazamientos
invertidos uno en relación con el otro. Cuando los dos se
traslapan en c), sus desplazamientos se cancelan parcialmente
uno a otro.
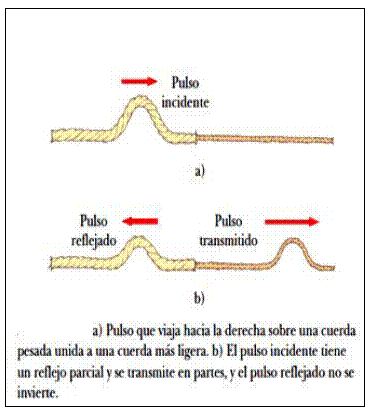
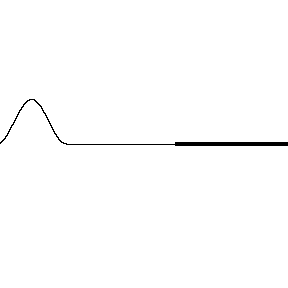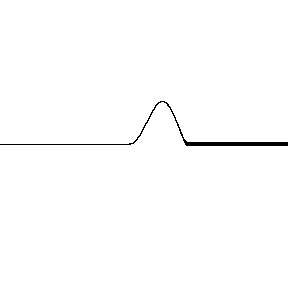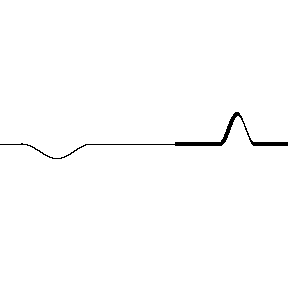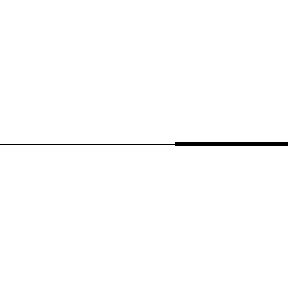
Interferencia en cuerdas de distinta densidad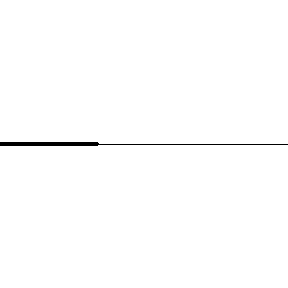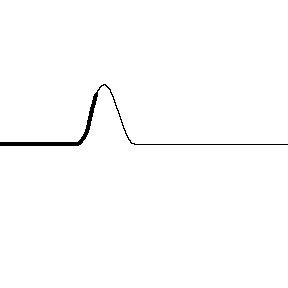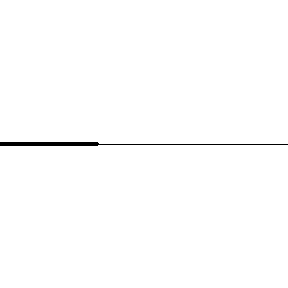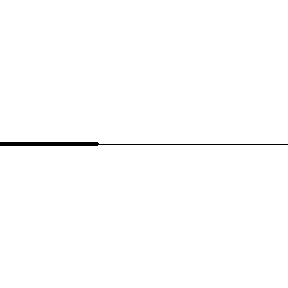
-
-
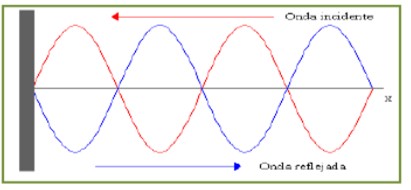
Si el sistema de partículas a través del cual se propagan las ondas periódicas tiene sus extremos fijos, como ocurre por ejemplo en las cuerdas de un instrumento, entonces las ondas se reflejan en ellos y se propagan por las cuerdas en sentido contrario.
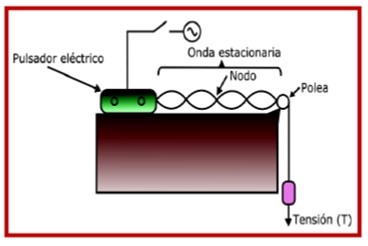 Un pulsador eléctrico,
unido a un cable, conduce a una
polea que sujeta una masa que causa tensión; cada nodo es propio de la
onda estacionaria.
Un pulsador eléctrico,
unido a un cable, conduce a una
polea que sujeta una masa que causa tensión; cada nodo es propio de la
onda estacionaria.
Una onda viajando en una cuerda puede encontrarse con otra que viaja en su misma dirección o en la opuesta. Cuando ello ocurre, se superponen, obteniéndose una tercera onda, que resulta de la suma de las anteriores (principio de superposición). Sin embargo luego de la superposición, se observa que ambas continúan su marcha como si nada hubiera ocurrido.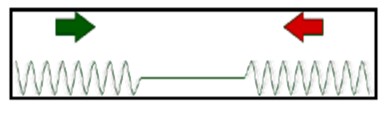 Entre estas ondas se
produce interferencia y de tal modo
que la cuerda o el sistema presenta
puntos que quedan sin vibrar y puntos que oscilan con amplitud máxima.
Los primeros se llaman nodos y los
segundos, vientres o
antinodos.
Entre estas ondas se
produce interferencia y de tal modo
que la cuerda o el sistema presenta
puntos que quedan sin vibrar y puntos que oscilan con amplitud máxima.
Los primeros se llaman nodos y los
segundos, vientres o
antinodos.
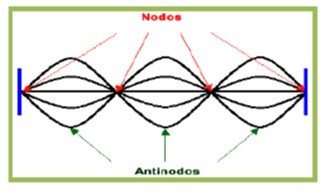
En cada nodo ocurre una interferencia destructiva y en cada antinodo una interferencia constructiva.
La distancia entre dos nodos o dos vientres consecutivos es de una semilongitud de onda.Si la onda resultante presenta interferencia puede producirse también nodos en los extremos, constituye una onda llamada estacionaria. En una onda estacionaria no se transporta energía de un punto a otro, a diferencia de las ondas viajeras. De ahí la existencia de nodos en ella.
Así pues, para que se produzcan ondas estacionarias es necesario que los extremos de la cuerda o del sistema sean nodos de la onda, y la condición para que ello ocurra es que la longitud de la cuerda o del sistema debe ser un múltiplo entero de una semi longitud de onda.
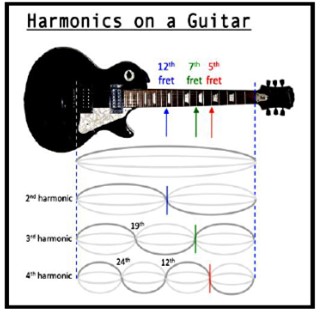
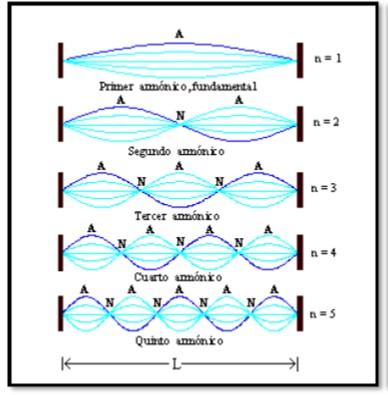 Un ejemplo de ondas
estacionarias lo encontramos en las cuerdas de los
instrumentos musicales. Los extremos
de las cuerdas se hallan siempre fijos, de modo que las
ondas que se establecen en ellas
rebotan instalando ondas viajeras que viajan con
sentidos opuestos.
Un ejemplo de ondas
estacionarias lo encontramos en las cuerdas de los
instrumentos musicales. Los extremos
de las cuerdas se hallan siempre fijos, de modo que las
ondas que se establecen en ellas
rebotan instalando ondas viajeras que viajan con
sentidos opuestos.
Al superponerse, aparecen las ondas estacionarias.
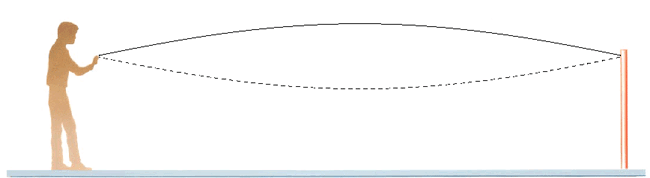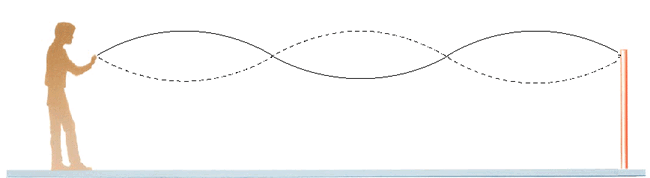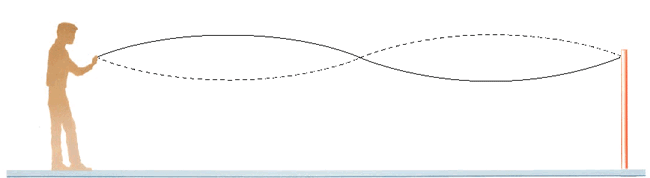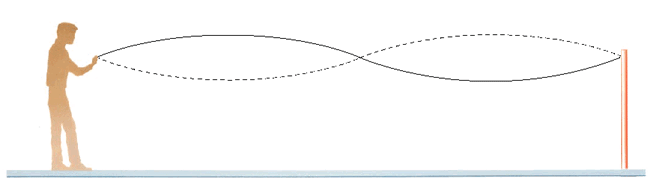
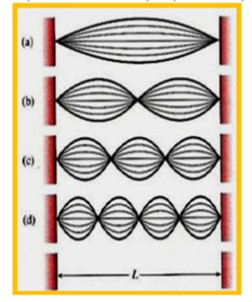 - En (a), modo n=1 se tiene
primer armónico, o frecuencia fundamental, donde su longitud de onda es:
- En (a), modo n=1 se tiene
primer armónico, o frecuencia fundamental, donde su longitud de onda es:
λ1= 2 L

- En (b), modo n=2 se tiene segundo armónico, donde su longitud de onda es:
λ2= L

- En (c), modo n=3 se tiene tercer armónico, donde su longitud de onda es:
λ3= 2/3 L
- En (d), modo n=4 se tiene cuarto armónico, donde su longitud de onda es:
λ4= L/2
En general para una onda estacionaria se puede señalar:
- La frecuencia del modo enésimo es n veces la frecuencia del modo fundamental fn= n·fo
- La distancia entre dos nodos consecutivos es λ/2
- La distancia entre un nodo y antinodo consecutivo es λ/4
- La rapidez de la onda se mantiene constante, a menos que cambie la tensión.
- A mayor modo de vibración mayor frecuencia y menor longitud de onda.-
Juego
-
-
-
Recurso
-
Recurso
-
-
-
Cuestionario
-